This thesis explores the intersection of deep learning and probabilistic machine learning to enhance the capabilities of artificial intelligence. It addresses the limitations of Gaussian processes (GPs) in practical applications, particularly in comparison to neural networks (NNs), and proposes advancements such as improved approximations and a novel formulation of Bayesian optimization (BO) that seamlessly integrates deep learning methods. The contributions aim to enrich the interplay between deep learning and probabilistic ML, advancing the foundations of AI and fostering the development of more capable and reliable automated decision-making systems.

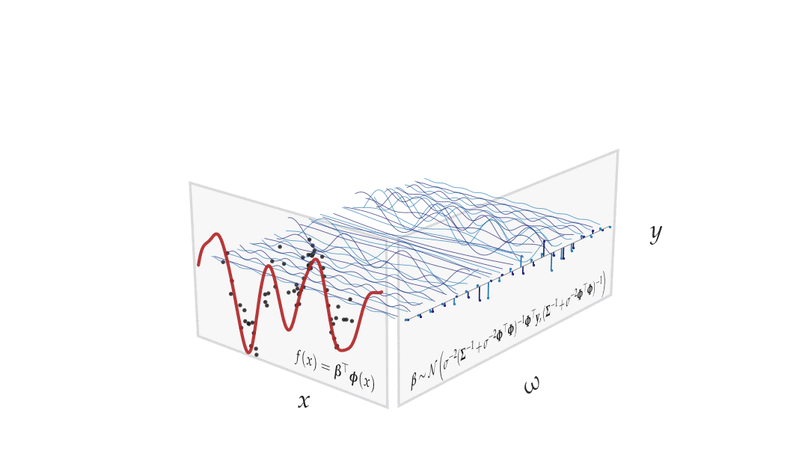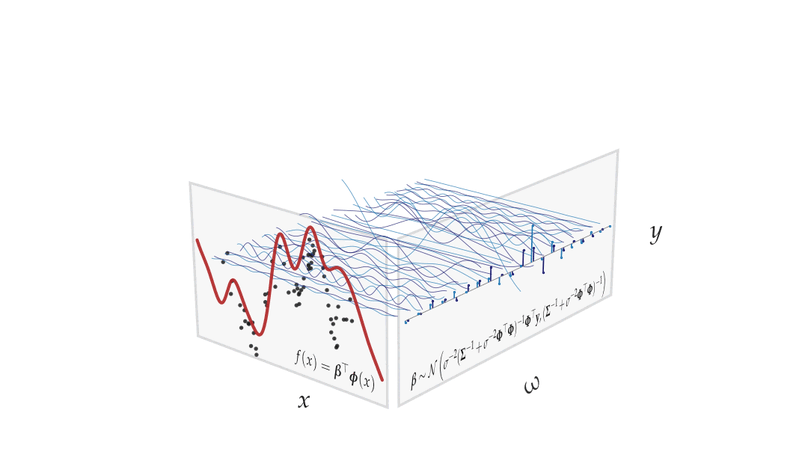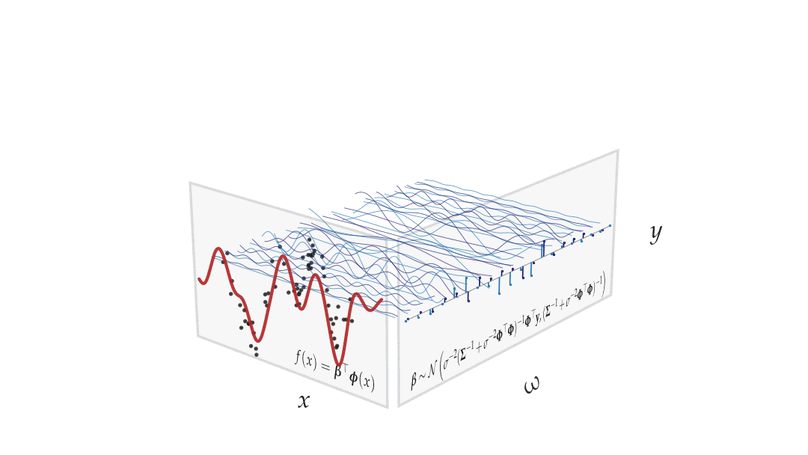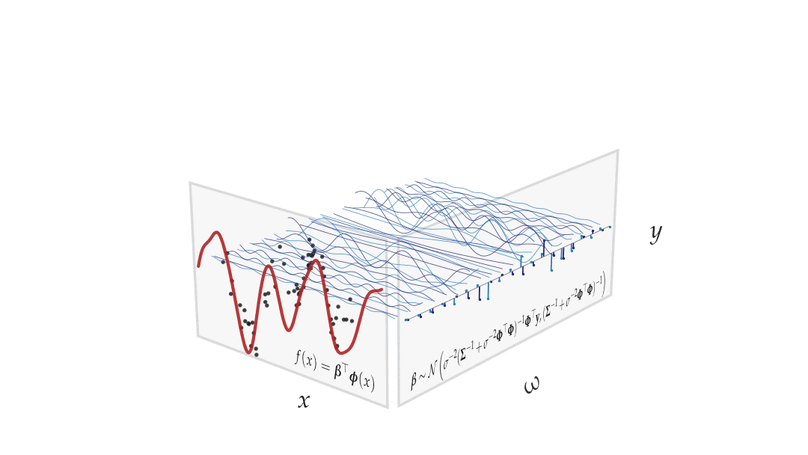
Despite their many desirable properties, Gaussian processes (GPs) are often compared unfavorably to deep neural networks (NNs) for lacking the ability to learn representations. Recent efforts to bridge the gap between GPs and deep NNs have yielded a new class of inter-domain variational GPs in which the inducing variables correspond to hidden units of a feedforward NN. In this work, we examine some practical issues associated with this approach and propose an extension that leverages the orthogonal decomposition of GPs to mitigate these limitations. In particular, we introduce spherical inter-domain features to construct more flexible data-dependent basis functions for both the principal and orthogonal components of the GP approximation and show that incorporating NN activation features under this framework not only alleviates these shortcomings but is more scalable than alternative strategies. Experiments on multiple benchmark datasets demonstrate the effectiveness of our approach.

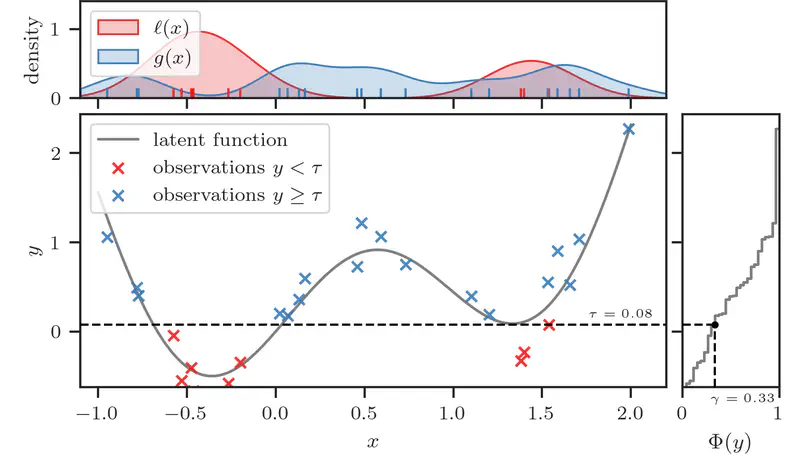
We reformulate the computation of the acquisition function in Bayesian optimization (BO) as a probabilistic classification problem, providing advantages in scalability, flexibility, and representational capacity, while casting aside the limitations of tractability constraints on the model.

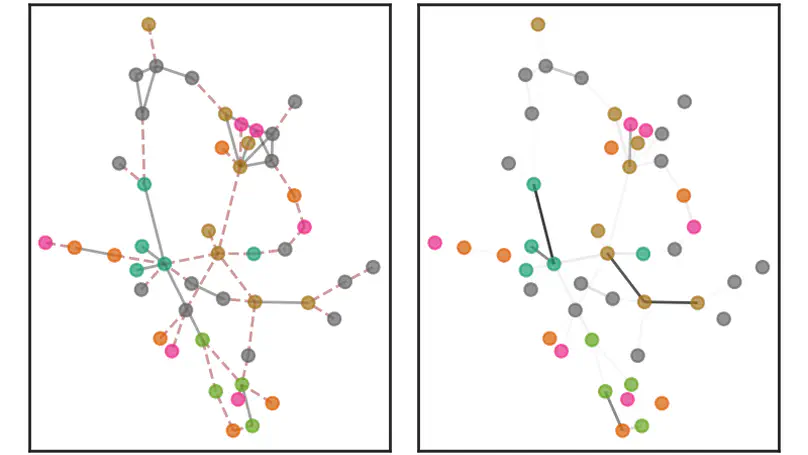
Our proposed framework uses a joint probabilistic model and stochastic variational inference to improve the performance and robustness of graph convolutional networks (GCNs) in scenarios without input graph data, outperforming state-of-the-art algorithms on semi-supervised classification tasks.

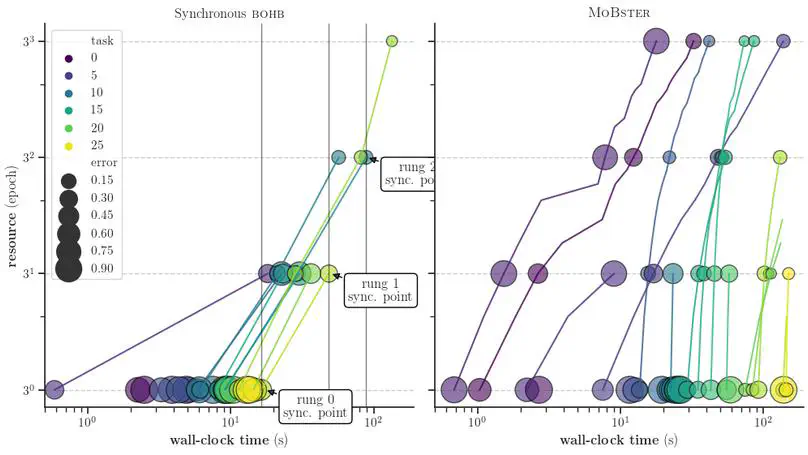
We introduce a model-based method for asynchronous multi-fidelity hyperparameter and neural architecture search that combines the strengths of asynchronous Hyperband and Gaussian process-based Bayesian optimization, achieving substantial speed-ups over current state-of-the-art methods on challenging benchmarks for tabular data, image classification, and language modeling.

A short and practical guide to efficiently computing the Cholesky decomposition of matrices perturbed by low-rank updates

One weird trick to make exact inference in Bayesian logistic regression tractable.

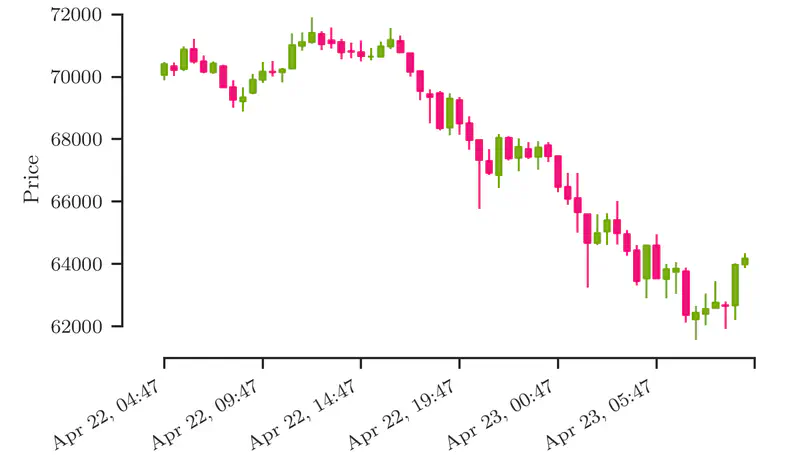
This series explores market data provided by official API from Binance, one of the world’s largest cryptocurrency exchanges, using Python. In this post we examine various useful ways to visualize the recent and historical trades.

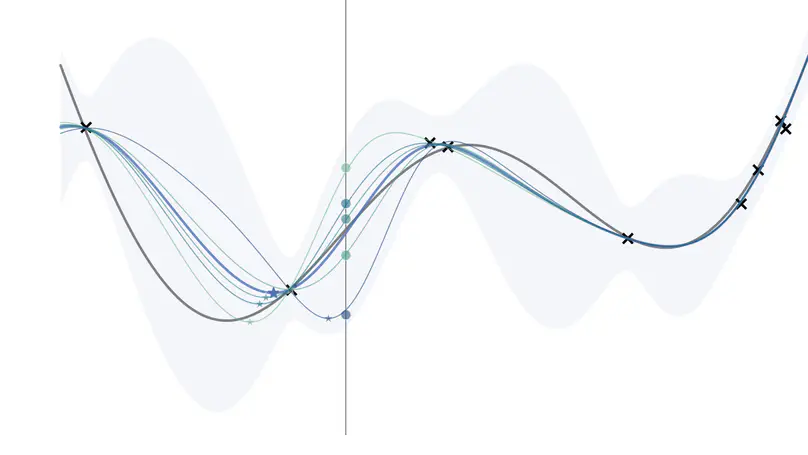
A short illustrated reference guide to the Knowledge Gradient acquisition function with an implementation from scratch in TensorFlow Probability.

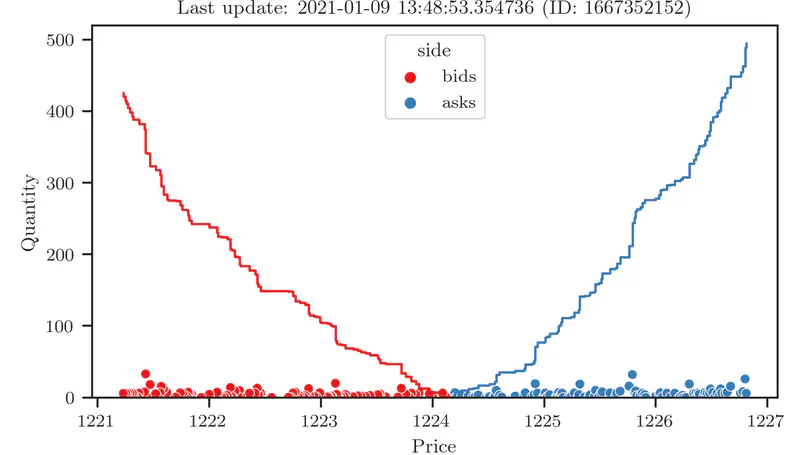
This series explores market data provided by official API from Binance, one of the world’s largest cryptocurrency exchanges, using Python. In this post we examine various useful ways to visualize the orderbook.

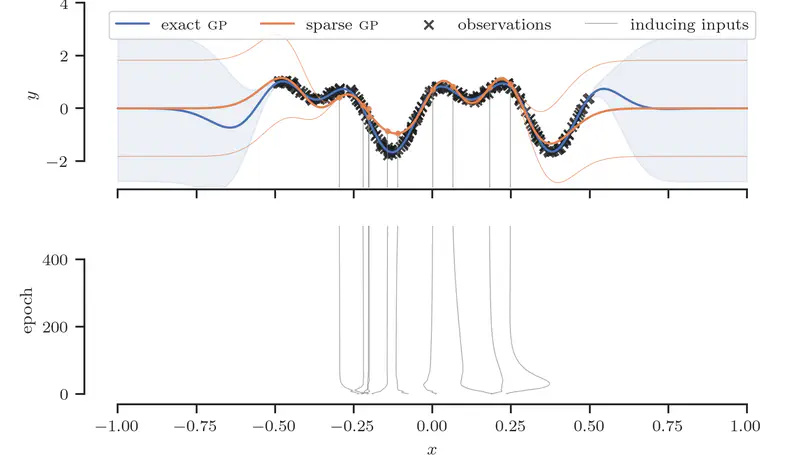
A summary of notation, identities and derivations for the sparse variational Gaussian process (SVGP) framework.

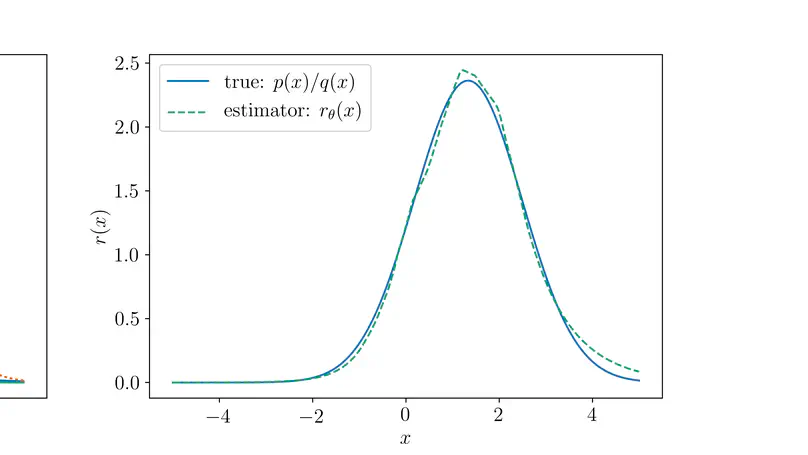
This post demonstrates how to approximate the KL divergence (in fact, any f-divergence) between implicit distributions, using density ratio estimation by probabilistic classification.

We illustrate how to build complicated probability distributions in a modular fashion using the Bijector API from TensorFlow Probability.