A Primer on Pólya-gamma Random Variables - Part II: Bayesian Logistic Regression
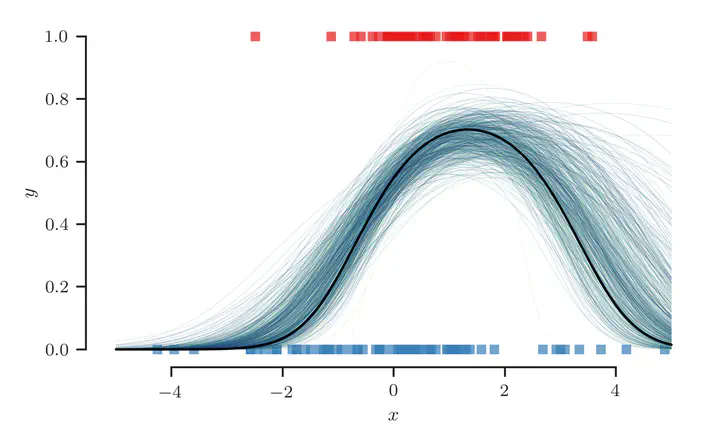
Table of Contents
Binary Classification
Consider the usual set-up for a binary classification problem: for some input $\mathbf{x} \in \mathbb{R}^{D}$, predict its binary label $y \in \{ 0, 1 \}$ given observations consisting of a feature matrix $\mathbf{X} = [ \mathbf{x}_1 \cdots \mathbf{x}_N ]^{\top} \in \mathbb{R}^{N \times D}$ and a target vector $\mathbf{y} = [ y_1 \cdots y_N ]^{\top} \in \{ 0, 1 \}^N$.
Model – Bayesian Logistic Regression
Recall the standard Bayesian logistic regression model:
Likelihood
Let $f: \mathbb{R}^{D} \to \mathbb{R}$ denote the real-valued latent function, sometimes referred to as the nuisance function, and let $f_n = f(\mathbf{x}_n)$ be the function value corresponding to observed input $\mathbf{x}_n$. The distribution over the observed variable $y_n$ is assumed to be governed by the latent variable $f_n$. In particular, the observed target vectors $\mathbf{y}$ are related to $\mathbf{f}$, the column vector of latent variables $\mathbf{f} = [f_1, \dotsc, f_N]^{\top}$, through the likelihood, or observation model, defined as $$ p(\mathbf{y} | \mathbf{f}) \doteq \prod_{n=1}^N p(y_n | f_n), $$ where $$ p(y_n | f_n) = \mathrm{Bern}(y_n | \sigma(f_n)) = \sigma(f_n)^{y_n} \left (1 - \sigma(f_n) \right )^{1 - y_n}, $$ and $\sigma(u) = \left ( 1 + \exp(-u) \right )^{-1}$ is the logistic sigmoid function.
Prior
For the sake of generality we discuss both the weight-space and function-space views of Bayesian logistic regression. In both cases, we consider a prior distribution in the form of a multivariate Gaussian $\mathcal{N}(\mathbf{m}, \mathbf{S}^{-1})$, whether it be over the weights or the function values themselves.
Weight-space
In the weight-space view, sometimes referred to as linear logistic
regression, we assume a priori that the latent function takes the form
$$
f(\mathbf{x}) = \boldsymbol{\beta}^{\top} \mathbf{x},
\qquad
\boldsymbol{\beta} \sim \mathcal{N}(\mathbf{m}, \mathbf{S}^{-1}).
$$
In this case, we express vector of latent function
values as $\mathbf{f} = \mathbf{X} \boldsymbol{\beta}$
and the prior over the weights
as $p(\boldsymbol{\beta}) = \mathcal{N}(\mathbf{m}, \mathbf{S}^{-1})$.
Function-space
In the function-space view, we assume the function is distributed according to a Gaussian process (GP) with mean function $m(\mathbf{x})$ and covariance function $k(\mathbf{x}, \mathbf{x}’)$ $$ f(\mathbf{x}) \sim \mathcal{GP}\left(m(\mathbf{x}), k(\mathbf{x}, \mathbf{x}’)\right) $$ In this case, we express the prior over latent function values as $p(\mathbf{f} | \mathbf{X}) = \mathcal{N}(\mathbf{m}, \mathbf{K}_X)$, where $\mathbf{m} = m(\mathbf{X})$ and $\mathbf{K}_X = k(\mathbf{X}, \mathbf{X})$.
Inference and Prediction
Given some test input $\mathbf{x}_*$, we are interested in producing a probability distribution over predictions $p(y_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*)$. As we shall see, the procedure for computing this distribition is rife with intractabilities.
Specifically, we first marginalize out the uncertainty about the associated latent function value $f_*$, $$ p(y_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*) = \int \sigma(f_*) p(f_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*) \mathrm{d}f_* $$ where $p(f_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*)$ is the posterior predictive distribution. Solving this integral is intractable, but since it is one-dimensional, it can be approximated efficiently using Gauss-Hermite quadrature assuming $p(f_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*)$ is Gaussian.
But herein lies the real difficulty: the predictive $p(f_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*)$ is computed as $$ p(f_* | \mathbf{X}, \mathbf{y}, \mathbf{x}_*) = \int p(f_* | \mathbf{X}, \mathbf{x}_*, \mathbf{f}) p(\mathbf{f} | \mathbf{X}, \mathbf{y}) \mathrm{d}\mathbf{f}, $$ where $p(\mathbf{f} | \mathbf{X}, \mathbf{y}) = \frac{p(\mathbf{y} | \mathbf{f}) p(\mathbf{f} | \mathbf{X})}{p(\mathbf{y} | \mathbf{X})} \propto p(\mathbf{y} | \mathbf{f}) p(\mathbf{f} | \mathbf{X})$ is the posterior over latent function values at the observed points, which is analytically intractable because a Gaussian prior is not conjugate to the Bernoulli likelihood.
To overcome this intractability, one must typically resort to approximate inference methods such as the Laplace approximation1, variational inference (VI)2, expectation propagation (EP)3 and sampling-based approximations such as Markov Chain Monte Carlo (MCMC).
Augmented Model
Instead of appealing to approximate inference methods, let us consider an augmentation strategy that works by introducing auxiliary variables to the model4.
In particular, we introduce auxiliary variables $\boldsymbol{\omega}$ and define the augmented or joint likelihood that factorizes as $$ p(\mathbf{y}, \boldsymbol{\omega} | \mathbf{f}) = p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) p(\boldsymbol{\omega}), $$ where $p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})$ is the conditional likelihood, a likelihood that is conditioned on the auxiliary variables $\boldsymbol{\omega}$, and $p(\boldsymbol{\omega})$ is the prior. Specifically, we wish to define $p(\boldsymbol{\omega})$ and $p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})$ for which the following two properties hold:
- Marginalizing out $\boldsymbol{\omega}$ recovers the original observation model $$ \int \underbrace{p(\mathbf{y}, \boldsymbol{\omega} | \mathbf{f})}_\text{joint likelihood} d\boldsymbol{\omega} = \int \underbrace{p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})}_\text{conditional likelihood} p(\boldsymbol{\omega}) d\boldsymbol{\omega} = \underbrace{p(\mathbf{y} | \mathbf{f})}_\text{original likelihood} $$
- A Gaussian prior $p(\mathbf{f})$ is conjugate to the conditional likelihood $p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})$.
Likelihood conditioned on auxiliary variables
First, let us define a conditional likelihood that factorize as $$ p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) = \prod_{n=1}^n p(y_n | f_n, \omega_n), $$ where each factor is defined as $$ p(y_n | f_n, \omega_n) \doteq \frac{1}{2} \exp{\left \{ - \frac{\omega_n}{2} \left ( f_n^2 - 2 f_n \frac{\kappa_n}{\omega_n} \right ) \right \}} $$ for $\kappa_n = y_n - \frac{1}{2}$.
Prior over auxiliary variables
Second, let us define a prior over auxiliary variables $\boldsymbol{\omega}$ that factorize as $$ p(\boldsymbol{\omega}) = \prod_{n=1}^N p(\omega_n) $$ where each factor $p(\omega_n)$ is a Pólya-gamma density $$ p(\omega_n) = \mathrm{PG}(\omega_n | 1, 0), $$ defined as an infinite convolution of gamma distributions :
Pólya-gamma density (Polson et al. 2013)
A random variable $\omega$ has a Pólya-gamma distribution with parameters $b > 0$ and $c \in \mathbb{R}$, denoted $\omega \sim \mathrm{PG}(b, c)$, if $$ \omega \overset{D}{=} \frac{1}{2 \pi^2} \sum_{k=1}^{\infty} \frac{g_k}{\left (k - \frac{1}{2} \right )^2 + \left ( \frac{c}{2\pi} \right )^2} $$ where the $g_k \sim \mathrm{Ga}(b, 1)$ are independent gamma random variables (and where $\overset{D}{=}$ denotes equality in distribution).
Property I: Recovering the original model
First we show that we can recover the original likelihood $p(y_n | f_n)$ by integrating out $\boldsymbol{\omega}$. Before we proceed, note that the $p(y_n | f_n)$ can be expressed more succinctly as $$ p(y_n | f_n) = \frac{e^{y_n f_n}}{1 + e^{f_n}}. $$ Refer to Appendix I for derivations. Next, note the following property of Pólya-gamma variables:
Laplace transform of the Pólya-gamma density (Polson et al. 2013)
Based on the Laplace transform
of the Pólya-gamma density function, we can derive the following relationship:
$$
\frac{\left (e^{u} \right )^a}{\left (1 + e^{u} \right )^b} =
\frac{1}{2^b} \exp{(\kappa u)}
\int_0^\infty \exp{\left ( - \frac{u^2}{2} \omega \right )}
p(\omega) d\omega,
$$
where $\kappa = a - \frac{b}{2}$ and $p(\omega) = \mathrm{PG}(\omega | b, 0)$.
Therefore, by substituting $\kappa = \kappa_n, a = y_n, b = 1$ and $u = f_n$ we get $$ \begin{align*} \int p(y_n, \omega_n | f_n) d\omega_n &= \int p(y_n | f_n, \omega_n) p(\omega_n) d\omega_n \newline &= \frac{1}{2} \int \exp{\left \{ - \frac{\omega_n}{2} \left (f_n^2 - 2 f_n \frac{\kappa_n}{\omega_n} \right ) \right \}} p(\omega_n) d\omega_n \newline &= \frac{1}{2} \exp{(\kappa_n f_n)} \int \exp{\left ( - \frac{f_n^2}{2} \omega_n \right )} p(\omega_n) d\omega_n \newline &= \frac{\left (e^{f_n} \right )^{y_n}}{1 + e^{f_n}} = p(y_n | f_n) \end{align*} $$ as required.
Property II: Gaussian-Gaussian conjugacy
Let us define the diagonal matrix $\boldsymbol{\Omega} = \mathrm{diag}(\omega_1 \cdots \omega_n)$ and vector $\mathbf{z} = \boldsymbol{\Omega}^{-1} \boldsymbol{\kappa}$. More simply, $\mathbf{z}$ is the vector with $n$th element $z_n = {\kappa_n} / {\omega_n}$. Hence, by completing the square, the per-datapoint conditional likelihood $p(y_n | f_n, \omega_n)$ above can be written as $$ \begin{align*} p(y_n | f_n, \omega_n) & \propto \exp{\left \{ - \frac{\omega_n}{2} \left (f_n - \frac{\kappa_n}{\omega_n} \right )^2 \right \}} \newline & = \exp{\left \{ - \frac{\omega_n}{2} \left (f_n - z_n \right )^2 \right \}} \end{align*} $$ Importantly, this implies that the conditional likelihood over all variables $p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})$ is simply a multivariate Gaussian distribution up to a constant factor $$ p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) \propto \mathcal{N}\left (\boldsymbol{\Omega}^{-1} \boldsymbol{\kappa} | \mathbf{f}, \boldsymbol{\Omega}^{-1} \right ). $$ Refer to Appendix II for derivations. Therefore, a Gaussian prior $p(\mathbf{f})$ is conjugate to the conditional likelihood $p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega})$, which leads to $p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega})$, the posterior over $\mathbf{f}$ conditioned on the auxiliary latent variables $\boldsymbol{\omega}$, also being a Gaussian—a property that will prove crucial to us in the next section.
Inference (Gibbs sampling)
We wish to compute the posterior distribution $p(\mathbf{f}, \boldsymbol{\omega} | \mathbf{y})$, the distribution over the hidden variables $(\mathbf{f}, \boldsymbol{\omega})$ conditioned on the observed variables $\mathbf{y}$. To produce samples from this distribution $$ (\mathbf{f}^{(t)}, \boldsymbol{\omega}^{(t)}) \sim p(\mathbf{f}, \boldsymbol{\omega} | \mathbf{y}), $$ we can readily apply Gibbs sampling5, an MCMC algorithm that can be seen as a special case of the Metropolis-Hastings algorithm.
Each step of the Gibbs sampling procedure involves replacing the value of one of the variables by a value drawn from the distribution of that variable conditioned on the values of the remaining variables. Specifically, we proceed as follows. At step $t$, we have values $\mathbf{f}^{(t-1)}, \boldsymbol{\omega}^{(t-1)}$ sampled from the previous step.
- We first replace $\mathbf{f}^{(t-1)}$ by a new value $\mathbf{f}^{(t)}$ by sampling from the conditional distribution $p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega}^{(t-1)})$, $$ \mathbf{f}^{(t)} \sim p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega}^{(t-1)}). $$
- Then we replace $\boldsymbol{\omega}^{(t-1)}$ by $\boldsymbol{\omega}^{(t)}$ by sampling from the conditional distribution $p(\boldsymbol{\omega}| \mathbf{f}^{(t)})$, $$ \boldsymbol{\omega}^{(t)} \sim p(\boldsymbol{\omega}| \mathbf{f}^{(t)}), $$ where we’ve used $\mathbf{f}^{(t)}$, the new value for $\mathbf{f}$ from step 1, straight away in the current step. Note that we’ve dropped the conditioning on $\mathbf{y}$, since $\boldsymbol{\omega}$ does not a posteriori depend on this variable.
We then proceed in like manner, cycling between the two variables in turn until some convergence criterion is met.
Suffice it to say, this requires us to first compute the conditional posteriors $p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega})$ and $p(\boldsymbol{\omega}| \mathbf{f})$, the calculation of which will be the subject of the next two subsections.
Posterior over latent function values
The posterior over the latent function values $\mathbf{f}$ conditioned on the auxiliary latent variables $\boldsymbol{\omega}$ is $$ p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega}) = \mathcal{N}(\mathbf{f} | \boldsymbol{\mu}, \boldsymbol{\Sigma}), $$ where $$ \boldsymbol{\mu} = \boldsymbol{\Sigma} \left ( \mathbf{S} \mathbf{m} + \boldsymbol{\kappa} \right ) \quad \text{and} \quad \boldsymbol{\Sigma} = \left (\mathbf{S} + \boldsymbol{\Omega} \right )^{-1}. $$
We readily obtain $\boldsymbol{\mu}$ and $\boldsymbol{\Sigma}$ by noting, as alluded to earlier, that $$ p(\mathbf{f}) = \mathcal{N}(\mathbf{m}, \mathbf{S}^{-1}), \qquad \text{and} \qquad p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) \propto \mathcal{N}\left (\boldsymbol{\Omega}^{-1} \boldsymbol{\kappa} | \mathbf{f}, \boldsymbol{\Omega}^{-1} \right ). $$ Thereafter, we can appeal to the following elementary properties of Gaussian conditioning and perform some pattern-matching substitutions:
Marginal and Conditional Gaussians (Bishop, Section 2.3.3, pg. 93)
Given a marginal Gaussian distribution for $\mathbf{b}$ and a conditional Gaussian distribution for $\mathbf{a}$ given $\mathbf{b}$ in the form
$$ \begin{align*} p(\mathbf{b}) & = \mathcal{N}(\mathbf{b} | \mathbf{m}, \mathbf{S}^{-1}) \newline p(\mathbf{a} | \mathbf{b}) & = \mathcal{N}(\mathbf{a} | \mathbf{W} \mathbf{b}, \boldsymbol{\Psi}^{-1}) \end{align*} $$ the marginal distribution of $\mathbf{a}$ and the conditional distribution of $\mathbf{b}$ given $\mathbf{a}$ are given by \begin{align*} p(\mathbf{a}) & = \mathcal{N}(\mathbf{a} | \mathbf{W} \mathbf{m}, \boldsymbol{\Psi}^{-1} + \mathbf{W} \mathbf{S}^{-1} \mathbf{W}^{\top}) \newline p(\mathbf{b} | \mathbf{a}) & = \mathcal{N}(\mathbf{b} | \boldsymbol{\mu}, \boldsymbol{\Sigma}) \end{align*} where $$ \boldsymbol{\mu} = \boldsymbol{\Sigma} \left ( \mathbf{W}^{\top} \boldsymbol{\Psi} \mathbf{a} + \mathbf{S} \mathbf{m} \right ), \quad \text{and} \quad \boldsymbol{\Sigma} = \left (\mathbf{S} + \mathbf{W}^{\top} \boldsymbol{\Psi} \mathbf{W}\right )^{-1}. $$
Note that we also could have derived this directly without resorting to the formulae above by reducing the product of two exponential-quadratic functions in $p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega}) \propto p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) p(\mathbf{f})$ into a single exponential-quadratic function up to a constant factor. It would, however, have been rather tedious and mundane.
Example: Gaussian process prior
To make this more concrete, let us revisit the Gaussian process prior we discussed earlier, namely, $$ p(\mathbf{f} | \mathbf{X}) = \mathcal{N}(\mathbf{m}, \mathbf{K}_X). $$ By substituting $\mathbf{S}^{-1} = \mathbf{K}_X$ from before, we obtain $$ p(\mathbf{f} | \mathbf{y}, \boldsymbol{\omega}) = \mathcal{N}(\mathbf{f} | \boldsymbol{\Sigma} \left ( \mathbf{K}_X^{-1} \mathbf{m} + \boldsymbol{\kappa} \right ), \boldsymbol{\Sigma}), $$ where $\boldsymbol{\Sigma} = \left (\mathbf{K}_X^{-1} + \boldsymbol{\Omega} \right )^{-1}.$
Posterior over auxiliary variables
The posterior over the auxiliary latent variables $\boldsymbol{\omega}$ conditioned on the latent function values $\mathbf{f}$ factorizes as $$ p(\boldsymbol{\omega}| \mathbf{f}) = \prod_{n=1}^{N} p(\omega_n | f_n), $$ where each factor $$ p(\omega_n | f_n) = \frac{p(f_n, \omega_n)}{\int p(f_n, \omega_n) d\omega_n}. $$ Now, the joint factorizes as $p(f_n, \omega_n) = p(f_n | \omega_n) p(\omega_n)$ where $$ p(f_n | \omega_n) = \exp{\left (-\frac{f_n^2}{2}\omega_n \right )}, \quad \text{and} \quad p(\omega_n) = \mathrm{PG}(\omega_n | 1, 0). $$ Hence, by the exponential-tilting property of the Pólya-gamma distribution, we have $$ p(\omega_n | f_n) = \mathrm{PG}(\omega_n | 1, f_n) \propto \mathrm{PG}(\omega_n | 1, 0) \times \exp{\left (-\frac{f_n^2}{2}\omega_n \right )} = p(f_n, \omega_n). $$ We have omitted the normalizing constant $\int p(f_n, \omega_n) d\omega_n$ from our discussion for the sake of brevity. If you’re interested in calculating it, refer to Appendix III.
Implementation (Weight-space view)
Having presented the general form of an augmented model for Bayesian logistic regression, we now derive a simple instance of this model to tackle a synthetic one-dimensional classification problem. In this particular implementation, we make the following choices: (a) we incorporate a basis function to project inputs into a higher-dimensional feature space, and (b) we consider an isotropic Gaussian prior on the weights.
Synthetic one-dimensional classification problem
First we synthesize a one-dimensional classification problem for which the true class-membership probability $p(y = 1 | x)$ is both known and easy to compute. To this end, let us introduce the following one-dimensional Gaussians, $$ p(x) = \mathcal{N}(1, 1^2), \qquad \text{and} \qquad q(x) = \mathcal{N}(0, 2^2). $$
In code we can specify these as:
from scipy.stats import norm
p = norm(loc=1.0, scale=1.0)
q = norm(loc=0.0, scale=2.0)
We evenly draw a total of $N$ samples from both distributions:
>>> X_p, X_q = draw_samples(num_train, p, q, rate=0.5, random_state=random_state)
where the function draw_samples is defined as:
def draw_samples(num_samples, p, q, rate=0.5, random_state=None):
num_top = int(num_samples * rate)
num_bot = num_samples - num_top
X_top = p.rvs(size=num_top, random_state=random_state)
X_bot = q.rvs(size=num_bot, random_state=random_state)
return X_top, X_bot
The densities of both distributions and their and samples are shown in the figure below.
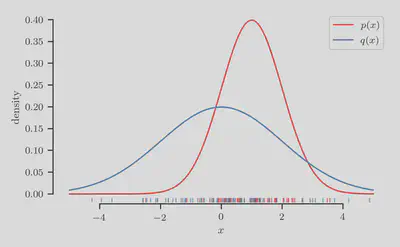
From these samples, let us now construct a classification dataset by assigning label $y = 1$ to inputs $x \sim p(x)$, and $y = 0$ to inputs $x \sim q(x)$.
>>> X_train, y_train = make_dataset(X_p, X_q)
where the function make_dataset is defined as:
def make_dataset(X_pos, X_neg):
X = np.expand_dim(np.hstack([X_pos, X_neg]), axis=-1)
y = np.hstack([np.ones_like(X_pos), np.zeros_like(X_neg)])
return X, y
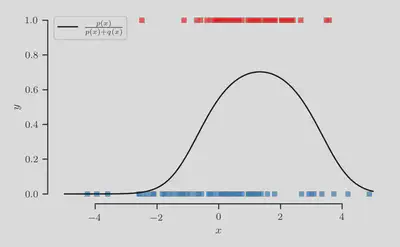
Crucially, the true class-membership probability is given exactly by $$ p(y = 1 | x) = \frac{p(x)}{p(x) + q(x)}, $$ thus providing a ground-truth yardstick by which to measure the quality of our resulting predictions.
The class-membership probability $p(y = 1 | x)$ is shown in the figure below as the black curve, along with the dataset $\mathcal{D}_N = \{(\mathbf{x}_n, y_n)\}_{n=1}^N$ where positive instances are colored red and negative instances are colored blue.
Prior
To increase the flexibility of our model, we introduce a basis
function $\phi: \mathbb{R}^{D} \to \mathbb{R}^{K}$ that projects
$D$-dimensional input vectors into a $K$-dimensional vector space.
Accordingly, we introduce matrix $\boldsymbol{\Phi} \in \mathbb{R}^{N \times K}$
such that the $n$th column of $\boldsymbol{\Phi}^{\top}$ consists of the
vector $\phi(\mathbf{x}_n)$.
Hence, we assume a priori that the latent function is of the form
$$
f(\mathbf{x}) = \boldsymbol{\beta}^{\top} \phi(\mathbf{x}),
$$
and express vector of latent function values
as $\mathbf{f} = \boldsymbol{\Phi} \boldsymbol{\beta}$.
In this example, we consider a simply polynomial basis function,
$$
\phi(x) = \begin{bmatrix} 1 & x & x^2 & \cdots & x^{K-1} \end{bmatrix}^{\top}.
$$
Therefore, we call:
>>> Phi = basis_function(X_train, degree=degree)
where the function basis_function is defined as:
def basis_function(x, degree=3):
return np.power(x, np.arange(degree))
Let us define the prior over weights as a simple isotropic Gaussian with precision $\alpha > 0$, $$ p(\boldsymbol{\beta}) = \mathcal{N}(\mathbf{0}, \alpha^{-1} \mathbf{I}), $$ and the prior over each local auxiliary latent variable as before, $$ p(\omega_n) = \mathrm{PG}(\omega_n | 1, 0). $$ Since we have analytic forms for the conditional posteriors, we don’t need to implement the priors explicitly. However, in order to initialize the Gibbs sampler, we may want to be able to sample from the prior. Let us do this using the prior over weights:
m = np.zeros(latent_dim)
alpha = 2.0 # prior precision
S_inv = np.eye(latent_dim) / alpha
# initialize `beta`
beta = random_state.multivariate_normal(mean=m, cov=S_inv)
or more simply:
alpha = 2.0 # prior precision
# initialize `beta`
beta = random_state.normal(size=latent_dim, scale=1/np.sqrt(alpha))
Conditional likelihood
The conditional likelihood is defined like before, except we instead condition on weights $\boldsymbol{\beta}$ and substitute occurrences of $\mathbf{f}$ with $\boldsymbol{\Phi} \boldsymbol{\beta}$, $$ p(\mathbf{y} | \boldsymbol{\beta}, \boldsymbol{\omega}) \propto \mathcal{N}\left (\boldsymbol{\Omega}^{-1} \boldsymbol{\kappa} | \boldsymbol{\Phi} \boldsymbol{\beta}, \boldsymbol{\Omega}^{-1} \right ). $$
Inference and Prediction
Posterior over latent function values
The posterior over the latent weights $\boldsymbol{\beta}$ conditioned on the auxiliary latent variables $\boldsymbol{\omega}$ is $$ p(\boldsymbol{\beta} | \mathbf{y}, \boldsymbol{\omega}) = \mathcal{N}(\boldsymbol{\beta} | \boldsymbol{\Sigma} \boldsymbol{\Phi}^{\top} \boldsymbol{\kappa}, \boldsymbol{\Sigma}), $$ where $$ \boldsymbol{\Sigma} = \left (\boldsymbol{\Phi}^{\top} \boldsymbol{\Omega} \boldsymbol{\Phi} + \alpha \mathbf{I} \right )^{-1}. $$
Let us implement the function that computes the mean and covariance of $p(\boldsymbol{\beta} | \mathbf{y}, \boldsymbol{\omega})$:
def conditional_posterior_weights(Phi, kappa, alpha, omega):
latent_dim = Phi.shape[-1]
Sigma_inv = (omega * Phi.T) @ Phi + alpha * np.eye(latent_dim)
mu = np.linalg.solve(Sigma_inv, Phi.T @ kappa)
Sigma = np.linalg.solve(Sigma_inv, np.eye(latent_dim))
return mu, Sigma
and a function to return samples from the multivariate Gaussian parameterized by this mean and covariance:
def gassian_sample(mean, cov, random_state=None):
random_state = check_random_state(random_state)
return random_state.multivariate_normal(mean=mean, cov=cov)
Posterior over auxiliary variables
The conditional posterior over the local auxiliary variable $\omega_n$ is defined as before, except we instead condition on weights $\boldsymbol{\beta}$ and substitute occurrences of $f_n$ with $\boldsymbol{\beta}^{\top} \phi(\mathbf{x}_n)$, $$ p(\omega_n | \boldsymbol{\beta}) \propto \mathrm{PG}(\omega_n | 1, \boldsymbol{\beta}^{\top} \phi(\mathbf{x}_n)). $$
Let us implement a function to compute the parameters of the posterior Polya-gamma distribution:
def conditional_posterior_auxiliary(Phi, beta):
c = Phi @ beta
b = np.ones_like(c)
return b, c
and accordingly a function to return samples from this distribution:
def polya_gamma_sample(b, c, pg=PyPolyaGamma()):
assert b.shape == c.shape, "shape mismatch"
omega = np.empty_like(b)
pg.pgdrawv(b, c, omega)
return omega
where we have imported the PyPolyaGamma object from
the pypolyagamma package:
from pypolyagamma import PyPolyaGamma
The pypolyagamma package can be installed via pip as usual:
$ pip install pypolyagamma
To provide some context, this package is a Cython port, created by S. Linderman, of the original R package BayesLogit authored by J. Windle that implements the method described in their paper on the efficient sampling of Pólya-gamma variables6.
Gibbs sampling
With these functions defined, we can define the Gibbs sampling procedure by the simple for-loop below:
# preprocessing
kappa = y_train - 0.5
Phi = basis_function(X_train, degree=degree)
# initialize `beta`
latent_dim = Phi.shape[-1]
beta = random_state.normal(size=latent_dim, scale=1/np.sqrt(alpha))
for i in range(num_iterations):
b, c = conditional_posterior_auxiliary(Phi, beta)
omega = polya_gamma_sample(b, c, pg=pg)
mu, Sigma = conditional_posterior_weights(Phi, kappa, alpha, omega)
beta = gassian_sample(mu, Sigma, random_state=random_state)
We now visualize the samples $(\boldsymbol{\beta}^{(t)}, \boldsymbol{\omega}^{(t)})$ produced by this procedure. In the figures that follow, we set the hues to be proportional to the step counter $t$ along a perceptually uniform colormap.
First, we show the sampled weight vector $\boldsymbol{\beta}^{(t)} \in \mathbb{R}^K$
where we have set $K = 3$.
We plot the $i$th entry $\beta_i^{(t)}$ against the $j$th entry $\beta_j^{(t)}$
for all $i < j$ and $0 < j < K$.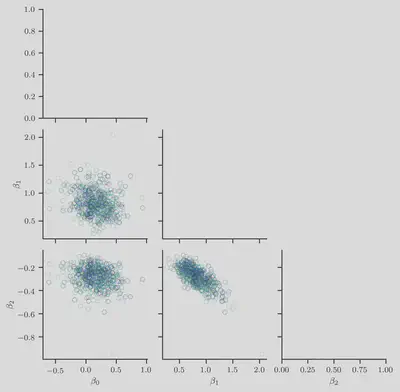
Second, we show the sampled auxiliary latent variables $\boldsymbol{\omega}^{(t)}$ by plotting the pairs $(x_n, \omega_n^{(t)})$.
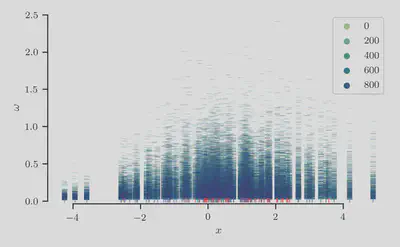
As expected, we find longer-tailed distributions in the variables $\omega_n$ that are associated with negative examples.
Finally, we plot the sampled class-membership probability predictions $$ \pi^{(t)}(\mathbf{x}) = \sigma(f^{(t)}(\mathbf{x})), \quad \text{where} \quad f^{(t)}(\mathbf{x}) = {\boldsymbol{\beta}^{(t)}}^{\top} \phi(\mathbf{x}), $$ in the figure below:
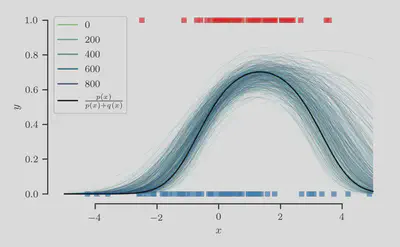
At least qualitatively, we find that the sampling procedure produces predictions that fit the true class-membership probability reasonably well.
Code
The full code is reproduced below:
import numpy as np
from scipy.stats import norm
from pypolyagamma import PyPolyaGamma
from .utils import (draw_samples, make_dataset, basis_function,
conditional_posterior_auxiliary, polya_gamma_sample,
conditional_posterior_weights, gassian_sample)
# constants
num_train = 128
num_iterations = 1000
degree = 3
alpha = 2.0 # prior precision
seed = 8888
random_state = np.random.RandomState(seed)
pg = PyPolyaGamma(seed=seed)
# generate dataset
p = norm(loc=1.0, scale=1.0)
q = norm(loc=0.0, scale=2.0)
X_p, X_q = draw_samples(num_train, p, q, rate=0.5, random_state=random_state)
X_train, y_train = make_dataset(X_p, X_q)
# preprocessing
kappa = y_train - 0.5
Phi = basis_function(X_train, degree=degree)
# initialize `beta`
latent_dim = Phi.shape[-1]
beta = random_state.normal(size=latent_dim, scale=1/np.sqrt(alpha))
for i in range(num_iterations):
b, c = conditional_posterior_auxiliary(Phi, beta)
omega = polya_gamma_sample(b, c, pg=pg)
mu, Sigma = conditional_posterior_weights(Phi, kappa, alpha, omega)
beta = gassian_sample(mu, Sigma, random_state=random_state)
where the module utils.py contains:
import numpy as np
from sklearn.utils import check_random_state
from pypolyagamma import PyPolyaGamma
def draw_samples(num_samples, p, q, rate=0.5, random_state=None):
num_top = int(num_samples * rate)
num_bot = num_samples - num_top
X_top = p.rvs(size=num_top, random_state=random_state)
X_bot = q.rvs(size=num_bot, random_state=random_state)
return X_top, X_bot
def make_dataset(X_pos, X_neg):
X = np.expand_dims(np.hstack([X_pos, X_neg]), axis=-1)
y = np.hstack([np.ones_like(X_pos), np.zeros_like(X_neg)])
return X, y
def basis_function(x, degree=3):
return np.power(x, np.arange(degree))
def polya_gamma_sample(b, c, pg=PyPolyaGamma()):
assert b.shape == c.shape, "shape mismatch"
omega = np.empty_like(b)
pg.pgdrawv(b, c, omega)
return omega
def gassian_sample(mean, cov, random_state=None):
random_state = check_random_state(random_state)
return random_state.multivariate_normal(mean=mean, cov=cov)
def conditional_posterior_weights(Phi, kappa, alpha, omega):
latent_dim = Phi.shape[-1]
eye = np.eye(latent_dim)
Sigma_inv = (omega * Phi.T) @ Phi + alpha * eye
mu = np.linalg.solve(Sigma_inv, Phi.T @ kappa)
Sigma = np.linalg.solve(Sigma_inv, eye)
return mu, Sigma
def conditional_posterior_auxiliary(Phi, beta):
c = Phi @ beta
b = np.ones_like(c)
return b, c
Bonus: Gibbs sampling with mutual recursion and generator delegation
The Gibbs sampling procedure naturally lends itself to implementations based
on mutual recursion.
Combining this with the yield from expression for generator delegation,
we can succinctly replace the for-loop with the following mutually recursive
functions:
def gibbs_sampler(beta, Phi, kappa, alpha, pg, random_state):
b, c = conditional_posterior_auxiliary(Phi, beta)
omega = polya_gamma_sample(b, c, pg=pg)
yield from gibbs_sampler_helper(omega, Phi, kappa, alpha, pg, random_state)
def gibbs_sampler_helper(omega, Phi, kappa, alpha, pg, random_state):
mu, Sigma = conditional_posterior_weights(Phi, kappa, alpha, omega)
beta = gassian_sample(mu, Sigma, random_state=random_state)
yield beta, omega
yield from gibbs_sampler(beta, Phi, kappa, alpha, pg, random_state)
Now you can use gibbs_sampler as a generator,
for example, to explicitly iterate over it in a for-loop:
for beta, omega in gibbs_sampler(beta, Phi, kappa, alpha, pg, random_state):
if stop_predicate:
break
# do something
pass
or by making use of itertools and other functional programming primitives:
from itertools import islice
# example: collect beta and omega samples into respective lists
betas, omegas = zip(*islice(gibbs_sampler(beta, Phi, kappa, alpha, pg, random_state), num_iterations))
There are a few obvious drawbacks to this implementation. First, while it may be a lot fun to write, it will probably not be as fun to read when you revisit it later on down the line. Second, you may occasionally find yourself hitting the maximum recursion depth before you have reached a sufficient number of iterations for the warm-up or “burn-in” phase to have been completed. It goes without saying, the latter can make this implementation a non-starter.
Links and Further Readings
- Papers:
- Blog posts:
- Pólya-Gamma Augmentation by G. Gundersen
- Code:
- pypolyagamma: A Python package by S. Linderman
- BayesLogit: An R package by J. Windle
Cite as:
@article{tiao2021polyagamma,
title = "{A} {P}rimer on {P}ólya-gamma {R}andom {V}ariables - {P}art II: {B}ayesian {L}ogistic {R}egression",
author = "Tiao, Louis C",
journal = "tiao.io",
year = "2021",
url = "https://tiao.io/post/polya-gamma-bayesian-logistic-regression/"
}
To receive updates on more posts like this, follow me on Twitter and GitHub!
Appendix
I
First, note that the logistic function can be written as $$ \sigma(u) = \frac{1}{1+e^{-u}} = \frac{e^u}{1+e^u} $$ Therefore, we have $$ \begin{align*} p(y_n | f_n) &= \left ( \frac{e^{f_n}}{1+e^{f_n}} \right )^{y_n} \left ( \frac{\left (1+e^{f_n} \right ) - e^{f_n}}{1+e^{f_n}} \right )^{1-y_n} \newline &= \left ( \frac{e^{f_n}}{1+e^{f_n}} \right )^{y_n} \left ( \frac{1}{1+e^{f_n}} \right )^{1-y_n} \newline &= \left (e^{f_n} \right )^{y_n} \left ( \frac{1}{1+e^{f_n}} \right )^{y_n} \left ( \frac{1}{1+e^{f_n}} \right )^{1-y_n} \newline &= \frac{e^{y_n f_n}}{1 + e^{f_n}} \end{align*} $$
II
The conditional likelihood factorizes as $$ \begin{align*} p(\mathbf{y} | \mathbf{f}, \boldsymbol{\omega}) &= \prod_{i=1}^n p(y_n | f_n, \omega_n) \newline &\propto \prod_{i=1}^n \exp{\left ( - \frac{\omega_n}{2} \left (f_n - z_n \right )^2 \right )} \newline &= \exp{\left ( - \frac{1}{2} \sum_{i=1}^n \omega_n \left (f_n - z_n \right )^2 \right )} \newline &= \exp{\left \{ - \frac{1}{2} (\mathbf{f} - \mathbf{z})^{\top} \boldsymbol{\Omega} (\mathbf{f} - \mathbf{z}) \right \}} \newline &\propto \mathcal{N}\left (\boldsymbol{\Omega}^{-1} \boldsymbol{\kappa} | \mathbf{f}, \boldsymbol{\Omega}^{-1} \right ) \end{align*} $$
III
We have omitted the normalizing constant $\int p(f_n, \omega_n) d\omega_n$ from our discussion for the sake of brevity since it is not required to carry out inference using Gibbs sampling. However, this is easy to compute, simply by referring to the Laplace transform of the $\mathrm{PG}(1, 0)$ distribution:
Laplace transform of the $\mathrm{PG}(1, 0)$ distribution (Polson et al. 2013)
The Laplace transform of the $\mathrm{PG}(1, 0)$ distribution is $$ \mathbb{E}_{\omega \sim \mathrm{PG}(1, 0)}[\exp(-\omega t)] = \frac{1}{\cosh{\left(\sqrt{\frac{t}{2}}\right)}}. $$
Hence, by making the substitution $t = \frac{f_n^2}{2}$, we obtain $$ \int p(f_n, \omega_n) d\omega_n = \int \exp{\left (-\frac{f_n^2}{2}\omega_n \right )} \mathrm{PG}(\omega_n | 1, 0) d\omega_n = \frac{1}{\cosh{\left(\frac{f_n}{2}\right)}}. $$ Therefore, we have $$ \begin{align*} p(\omega_n | f_n) & = \frac{p(f_n, \omega_n)}{\int p(f_n, \omega_n) d\omega_n} \newline & = \cosh{\left(\frac{f_n}{2}\right)} \exp{\left (-\frac{f_n^2}{2}\omega_n \right )} \mathrm{PG}(\omega_n | 1, 0) \newline & = \mathrm{PG}(\omega_n | 1, f_n). \end{align*} $$
MacKay, D. J. (1992). The Evidence Framework Applied to Classification Networks. Neural Computation, 4(5), 720-736. ↩︎
Jaakkola, T. S., & Jordan, M. I. (2000). Bayesian Parameter Estimation via Variational Methods. Statistics and Computing, 10(1), 25-37. ↩︎
Minka, T. P. (2001, August). Expectation Propagation for Approximate Bayesian Inference. In Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence (pp. 362-369). ↩︎
Polson, N. G., Scott, J. G., & Windle, J. (2013). Bayesian Inference for Logistic Models using Pólya–Gamma Latent Variables. Journal of the American Statistical Association, 108(504), 1339-1349. ↩︎ ↩︎
Geman, S., & Geman, D. (1984). Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence, (6), 721-741. ↩︎
Windle, J., Polson, N. G., & Scott, J. G. (2014). Sampling Pólya-gamma Random Variates: Alternate and Approximate Techniques. arXiv preprint arXiv:1405.0506. ↩︎
Wenzel, F., Galy-Fajou, T., Donner, C., Kloft, M., & Opper, M. (2019, July). Efficient Gaussian Process Classification using Pòlya-Gamma Data Augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 33, No. 01, pp. 5417-5424). ↩︎
Snell, J., & Zemel, R. (2020). Bayesian Few-Shot Classification with One-vs-Each Pólya-Gamma Augmented Gaussian Processes. arXiv preprint arXiv:2007.10417. ↩︎