Spherical Inducing Features for Orthogonally-Decoupled Gaussian Processes
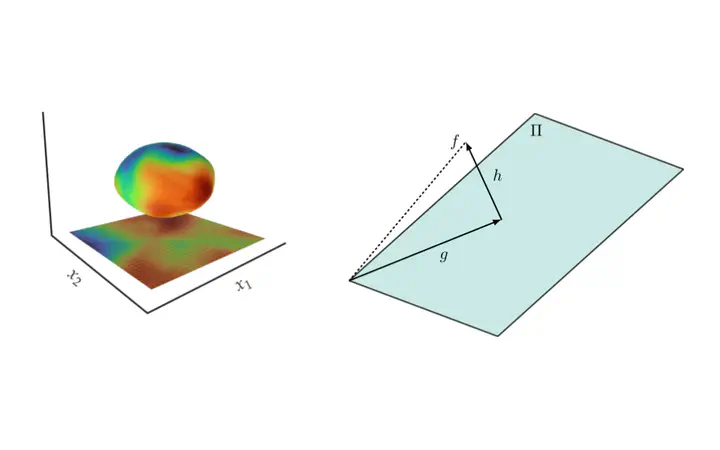Left: A single-layer feedforward neural network on the unit sphere projected onto a plane in 3D; Right: Decoupling of a GP as a sum of orthogonal GPsAbstract
Despite their many desirable properties, Gaussian processes (GPs) are often compared unfavorably to deep neural networks (NNs) for lacking the ability to learn representations. Recent efforts to bridge the gap between GPs and deep NNs have yielded a new class of inter-domain variational GPs in which the inducing variables correspond to hidden units of a feedforward NN. In this work, we examine some practical issues associated with this approach and propose an extension that leverages the orthogonal decomposition of GPs to mitigate these limitations. In particular, we introduce spherical inter-domain features to construct more flexible data-dependent basis functions for both the principal and orthogonal components of the GP approximation and show that incorporating NN activation features under this framework not only alleviates these shortcomings but is more scalable than alternative strategies. Experiments on multiple benchmark datasets demonstrate the effectiveness of our approach.
