Variational Inference for Graph Convolutional Networks in the Absence of Graph Data and Adversarial Settings
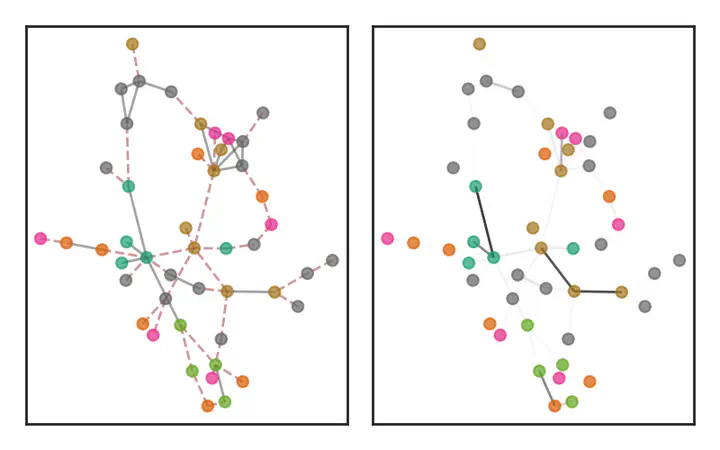Left: Observed graph. Edges of original graph are denoted by solid lines, while spuriously added edges are denoted by maroon dashed lines. Right: Resulting posterior probabilities over edges denoted by edge color opacity. With few exceptions, the posterior probabilities of the added edges are attenuated.Abstract
We propose a framework that lifts the capabilities of graph convolutional networks (GCNs) to scenarios where no input graph is given and increases their robustness to adversarial attacks. We formulate a joint probabilistic model that considers a prior distribution over graphs along with a GCN-based likelihood and develop a stochastic variational inference algorithm to estimate the graph posterior and the GCN parameters jointly. To address the problem of propagating gradients through latent variables drawn from discrete distributions, we use their continuous relaxations known as Concrete distributions. We show that, on real datasets, our approach can outperform state-of-the-art Bayesian and non-Bayesian graph neural network algorithms on the task of semi-supervised classification in the absence of graph data and when the network structure is subjected to adversarial perturbations.
This paper is a follow-up to our working paper, previously presented at the NeurIPS2019 Graph Representation Learning Workshop, now with significantly expanded experimental analyses.
