A Handbook for Sparse Variational Gaussian Processes
A summary of notation, identities and derivations for the sparse variational Gaussian process (SVGP) framework
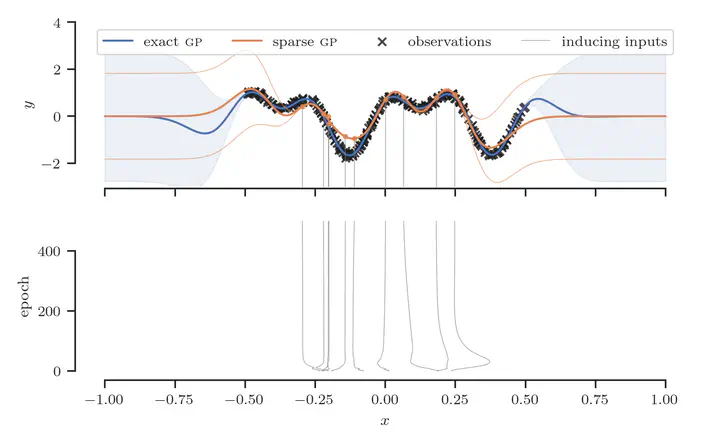
Table of Contents
In the sparse variational Gaussian process (SVGP) framework (Titsias, 2009)1, one augments the joint distribution $p(\mathbf{y}, \mathbf{f})$ with auxiliary variables $\mathbf{u}$ so that the joint becomes $$ p(\mathbf{y}, \mathbf{f}, \mathbf{u}) = p(\mathbf{y} | \mathbf{f}) p(\mathbf{f}, \mathbf{u}). $$ The vector $\mathbf{u} = \begin{bmatrix} u(\mathbf{z}_1) \cdots u(\mathbf{z}_M)\end{bmatrix}^{\top} \in \mathbb{R}^M$ consists of inducing variables, the latent function values corresponding to the inducing input locations contained in the matrix $\mathbf{Z} = \begin{bmatrix} \mathbf{z}_1 \cdots \mathbf{z}_M \end{bmatrix}^{\top} \in \mathbb{R}^{M \times D}$.
Prior
The joint distribution of the latent function values $\mathbf{f}$, and the inducing variables $\mathbf{u}$ according to the prior is $$ p(\mathbf{f}, \mathbf{u}) = \mathcal{N} \left ( \begin{bmatrix} \mathbf{f} \newline \mathbf{u} \end{bmatrix} ; \begin{bmatrix} \mathbf{0} \newline \mathbf{0} \end{bmatrix}, \begin{bmatrix} \mathbf{K}_\mathbf{ff} & \mathbf{K}_\mathbf{uf}^\top \newline \mathbf{K}_\mathbf{uf} & \mathbf{K}_\mathbf{uu} \end{bmatrix} \right ). $$ If we let the joint prior factorize as $$ p(\mathbf{f}, \mathbf{u}) = p(\mathbf{f} | \mathbf{u}) p(\mathbf{u}), $$ we can apply the rules of Gaussian conditioning to derive the marginal prior $p(\mathbf{u})$ and conditional prior $p(\mathbf{f} | \mathbf{u})$.
Marginal prior over inducing variables
The marginal prior over inducing variables is simply given by $$ p(\mathbf{u}) = \mathcal{N}(\mathbf{u} | \mathbf{0}, \mathbf{K}_\mathbf{uu}). $$
Gaussian process notation
We can express the prior over the inducing variable $u(\mathbf{z})$ at inducing input $\mathbf{z}$ as $$ p(u(\mathbf{z})) = \mathcal{GP}(0, k_{\theta}(\mathbf{z}, \mathbf{z}’)). $$
Conditional prior
First, let us define the vector-valued function $\boldsymbol{\psi}_\mathbf{u}: \mathbb{R}^{D} \to \mathbb{R}^{M}$ as $$ \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}) \triangleq \mathbf{K}_\mathbf{uu}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}), $$ where $\mathbf{k}_\mathbf{u}(\mathbf{x}) = k_{\theta}(\mathbf{Z}, \mathbf{x})$ denotes the vector of covariances between $\mathbf{x}$ and the inducing inputs $\mathbf{Z}$. Further, let $\boldsymbol{\Psi} \in \mathbb{R}^{M \times N}$ be the matrix containing values of function $\psi$ applied row-wise to the matrix of inputs $\mathbf{X} = \begin{bmatrix} \mathbf{x}_1 \cdots \mathbf{x}_N \end{bmatrix}^{\top} \in \mathbb{R}^{N \times D}$, $$ \boldsymbol{\Psi} \triangleq \begin{bmatrix} \psi(\mathbf{x}_1) \cdots \psi(\mathbf{x}_N) \end{bmatrix} = \mathbf{K}_\mathbf{uu}^{-1} \mathbf{K}_\mathbf{uf}. $$ Then, we can condition the joint prior distribution on the inducing variables to give $$ p(\mathbf{f} | \mathbf{u}) = \mathcal{N}(\mathbf{f} | \mathbf{m}, \mathbf{S}), $$ where the mean vector and covariance matrix are $$ \mathbf{m} = \boldsymbol{\Psi}^{\top} \mathbf{u}, \quad \text{and} \quad \mathbf{S} = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^{\top} \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi}. $$
Gaussian process notation
We can express the distribution over the function value $f(\mathbf{x})$ at input $\mathbf{x}$, given $\mathbf{u}$, that is, the conditional $p(f(\mathbf{x}) | \mathbf{u})$, as a Gaussian process: $$ p(f(\mathbf{x}) | \mathbf{u}) = \mathcal{GP}(m(\mathbf{x}), s(\mathbf{x}, \mathbf{x}’)), $$ with mean and covariance functions, $$ m(\mathbf{x}) = \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{u}, \quad \text{and} \quad s(\mathbf{x}, \mathbf{x}’) = k_{\theta}(\mathbf{x}, \mathbf{x}’) - \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu} \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}’). $$
Before moving on, we briefly highlight the important quantity, $$ \mathbf{Q}_\mathbf{ff} \triangleq \boldsymbol{\Psi}^{\top} \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi}, $$ which is sometimes referred to as the Nyström approximation of $\mathbf{K}_\mathbf{ff}$. It can be written as $$ \mathbf{Q}_\mathbf{ff} = \mathbf{K}_\mathbf{fu} \mathbf{K}_\textbf{uu}^{-1} \mathbf{K}_\mathbf{uf}. $$
Variational Distribution
We specify a joint variational distribution $q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})$ which factorizes as $$ q_{\boldsymbol{\phi}}(\mathbf{f}, \mathbf{u}) \triangleq p(\mathbf{f} | \mathbf{u}) q_{\boldsymbol{\phi}}(\mathbf{u}). $$ For convenience, let us specify a variational distribution that is also Gaussian, $$ q_{\boldsymbol{\phi}}(\mathbf{u}) \triangleq \mathcal{N}(\mathbf{u} | \mathbf{b}, \mathbf{W}\mathbf{W}^{\top}), $$ with variational parameters $\boldsymbol{\phi} = \{ \mathbf{W}, \mathbf{b} \}$. To obtain the corresponding marginal variational distribution over $\mathbf{f}$, we marginalize out the inducing variables $\mathbf{u}$, leading to $$ q_{\boldsymbol{\phi}}(\mathbf{f}) = \int q_{\boldsymbol{\phi}}(\mathbf{f}, \mathbf{u}) \, \mathrm{d}\mathbf{u} = \mathcal{N}(\mathbf{f} | \boldsymbol{\mu}, \mathbf{\Sigma}), $$ where $$ \boldsymbol{\mu} = \boldsymbol{\Psi}^\top \mathbf{b}, \quad \text{and} \quad \mathbf{\Sigma} = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^\top (\mathbf{K}_\mathbf{uu} - \mathbf{W}\mathbf{W}^{\top}) \boldsymbol{\Psi}. $$
Gaussian process notation
We can express the variational distribution over the function value $f(\mathbf{x})$ at input $\mathbf{x}$, that is, the marginal $q_{\boldsymbol{\phi}}(f(\mathbf{x}))$, as a Gaussian process: $$ q_{\boldsymbol{\phi}}(f(\mathbf{x})) = \mathcal{GP}(\mu(\mathbf{x}), \sigma(\mathbf{x}, \mathbf{x}’)), $$ with mean and covariance functions, $$ \mu(\mathbf{x}) = \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{b}, \quad \text{and} \quad \sigma(\mathbf{x}, \mathbf{x}’) = \kappa_{\theta}(\mathbf{x}, \mathbf{x}’) - \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) (\mathbf{K}_\mathbf{uu} - \mathbf{W}\mathbf{W}^{\top}) \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}’). $$
Whitened parameterization
Whitening is a powerful trick for stabilizing the learning of variational parameters that works by reducing correlations in the variational distribution (Murray & Adams, 2010; Hensman et al, 2015)2 3. Let $\mathbf{L}$ be the Cholesky factor of $\mathbf{K}_\mathbf{uu}$, i.e. the lower triangular matrix such that $\mathbf{L} \mathbf{L}^{\top} = \mathbf{K}_\mathbf{uu}$. Then, the whitened variational parameters are given by $$ \mathbf{W} \triangleq \mathbf{L} \mathbf{W}’, \quad \text{and} \quad \mathbf{b} \triangleq \mathbf{L} \mathbf{b}’, $$ with free parameters $\{ \mathbf{W}’, \mathbf{b}’ \}$. This leads to mean and covariance $$ \boldsymbol{\mu} = \boldsymbol{\Lambda}^\top \mathbf{b}’, \quad \text{and} \quad \mathbf{\Sigma} = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^\top (\mathbf{I}_M - {\mathbf{W}’} {\mathbf{W}’}^{\top}) \boldsymbol{\Lambda}, $$ where $$ \boldsymbol{\Lambda} \triangleq \mathbf{L}^\top \boldsymbol{\Psi} = \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf}. $$ Refer to Appendix I for derivations.
Gaussian process notation
The mean and covariance functions are now $$ \mu(\mathbf{x}) = \boldsymbol{\lambda}^\top(\mathbf{x}) \mathbf{b}’, \quad \text{and} \quad \sigma(\mathbf{x}, \mathbf{x}’) = k_{\theta}(\mathbf{x}, \mathbf{x}’) - \boldsymbol{\lambda}^\top(\mathbf{x}) (\mathbf{I}_M - \mathbf{W}’ {\mathbf{W}’}^{\top}) \boldsymbol{\lambda}(\mathbf{x}’), $$ where $$ \boldsymbol{\lambda}(\mathbf{x}) \triangleq \mathbf{L}^{\top} \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}) = \mathbf{L}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}). $$
For an efficient and numerically stable way to compute and evaluate the variational distribution $q_{\boldsymbol{\phi}}(\mathbf{f})$ at an arbitrary set of inputs, see Appendix II.
Inference
Preliminaries
We seek to approximate the exact posterior $p(\mathbf{f},\mathbf{u} \mid \mathbf{y})$ by an variational distribution $q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})$. To this end, we minimize the Kullback-Leibler (KL) divergence between $q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})$ and $p(\mathbf{f},\mathbf{u} \mid \mathbf{y})$, which is given by $$ \begin{align*} \mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) \mid\mid p(\mathbf{f},\mathbf{u} \mid \mathbf{y})] & = \mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}\left[\log{\frac{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}{p(\mathbf{f},\mathbf{u} \mid \mathbf{y})}}\right] \newline & = \log{p(\mathbf{y})} + \mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}\left[\log{\frac{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}{p(\mathbf{f},\mathbf{u}, \mathbf{y})}}\right] \newline & = \log{p(\mathbf{y})} - \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}), \end{align*} $$ where we’ve defined the evidence lower bound (ELBO) as $$ \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}) \triangleq \mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}\left[\log{\frac{p(\mathbf{f},\mathbf{u}, \mathbf{y})}{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}}\right]. $$ Notice that minimizing the KL divergence above is equivalent to maximizing the ELBO. Furthermore, the ELBO is a lower bound on the log marginal likelihood, since $$ \log{p(\mathbf{y})} = \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}) + \mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) \mid\mid p(\mathbf{f},\mathbf{u} \mid \mathbf{y})], $$ and the KL divergence is nonnegative. Therefore, we have $\log{p(\mathbf{y})} \geq \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z})$ with equality at $\mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) \mid\mid p(\mathbf{f},\mathbf{u} \mid \mathbf{y})] = 0 \Leftrightarrow q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) = p(\mathbf{f},\mathbf{u} \mid \mathbf{y})$.
Let us now focus our attention on the ELBO, which can be written as $$ \require{cancel} \begin{align*} \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}) & = \iint \log{\frac{p(\mathbf{f},\mathbf{u}, \mathbf{y})}{q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u})}} q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) \,\mathrm{d}\mathbf{f} \mathrm{d}\mathbf{u} \newline & = \iint \log{\frac{p(\mathbf{y} | \mathbf{f}) \bcancel{p(\mathbf{f} | \mathbf{u})} p(\mathbf{u})}{\bcancel{p(\mathbf{f} | \mathbf{u})} q_{\boldsymbol{\phi}}(\mathbf{u})}} q_{\boldsymbol{\phi}}(\mathbf{f},\mathbf{u}) \,\mathrm{d}\mathbf{f} \mathrm{d}\mathbf{u} \newline & = \int \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u}, \end{align*} $$ where we have made use of the previous definition $q_{\boldsymbol{\phi}}(\mathbf{f}, \mathbf{u}) = p(\mathbf{f} | \mathbf{u}) q_{\boldsymbol{\phi}}(\mathbf{u})$ and also introduced the definition $$ \Phi(\mathbf{y}, \mathbf{u}) \triangleq \exp{ \left ( \int \log{p(\mathbf{y} | \mathbf{f})} p(\mathbf{f} | \mathbf{u}) \,\mathrm{d}\mathbf{f} \right ) }. $$ It is straightforward to verify that the optimal variational distribution, that is, the distribution $q_{\boldsymbol{\phi}^{\star}}(\mathbf{u})$ at which the ELBO is maximized, satisfies $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) \propto \Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u}). $$ Refer to Appendix III for details. Specifically, after normalization, we have $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) = \frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{\mathcal{Z}}, $$ where $\mathcal{Z} \triangleq \int \Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u}) \,\mathrm{d}\mathbf{u}$. Plugging this back into the ELBO, we get $$ \require{cancel} \mathrm{ELBO}(\boldsymbol{\phi}^{\star}, \mathbf{Z}) = \int \log{\left (\bcancel{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})} \frac{\mathcal{Z}}{\bcancel{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}} \right )} q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} = \log{\mathcal{Z}}. $$
Gaussian Likelihoods – Sparse Gaussian Process Regression (SGPR)
Let us assume we have a Gaussian likelihood of the form $$ p(\mathbf{y} | \mathbf{f}) = \mathcal{N}(\mathbf{y} | \mathbf{f}, \beta^{-1} \mathbf{I}). $$ Then it is straightforward to show that $$ \log{\Phi(\mathbf{y}, \mathbf{u})} = \log{\mathcal{N}(\mathbf{y} | \mathbf{m}, \beta^{-1} \mathbf{I} )} - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}), $$ where $\mathbf{m}$ and $\mathbf{S}$ are defined as before, i.e. $\mathbf{m} = \boldsymbol{\Psi}^{\top} \mathbf{u}$ and $\mathbf{S} = \mathbf{K}_\textbf{ff} - \boldsymbol{\Psi}^{\top} \mathbf{K}_\textbf{uu} \boldsymbol{\Psi}$. Refer to Appendix IV for derivations.
Now, there are a few key objects of interest. First, the optimal variational distribution $q_{\boldsymbol{\phi}^{\star}}(\mathbf{u})$, which is required to compute the predictive distribution $q_{\boldsymbol{\phi}^{\star}}(\mathbf{f}) = \int p(\mathbf{f}|\mathbf{u}) q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) \, \mathrm{d}\mathbf{u}$, but which may also be of independent interest. Second, the ELBO, the objective with respect to which the inducing input locations $\mathbf{Z}$ are optimized.
The optimal variational distribution is given by $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) = \mathcal{N}(\mathbf{u} \mid \beta \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uf} \mathbf{y}, \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uu}), $$ where $$ \mathbf{M} \triangleq \mathbf{K}_\mathbf{uu} + \beta \mathbf{K}_\mathbf{uf} \mathbf{K}_\mathbf{fu}. $$ This can be verified by reducing the product of two exponential-quadratic functions in $\Phi(\mathbf{y}, \mathbf{u})$ and $p(\mathbf{u})$ into a single exponential-quadratic function up to a constant factor, an operation also known as “completing the square”. Refer to Appendix V for complete derivations.
This leads to the predictive distribution $$ \begin{align*} q_{\boldsymbol{\phi}^{\star}}(\mathbf{f}) & = \mathcal{N}\left(\beta \boldsymbol{\Psi}^\top \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi} \mathbf{y}, \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^\top (\mathbf{K}_\mathbf{uu} - \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uu} ) \boldsymbol{\Psi} \right) \\ & = \mathcal{N}\left(\beta \mathbf{K}_\mathbf{fu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uf} \mathbf{y}, \mathbf{K}_\mathbf{ff} - \mathbf{K}_\mathbf{fu} (\mathbf{K}_\mathbf{uu}^{-1} - \mathbf{M}^{-1}) \mathbf{K}_\mathbf{uf} \right). \end{align*} $$
The ELBO is given by $$ \mathrm{ELBO}(\boldsymbol{\phi}^{\star}, \mathbf{Z}) = \log \mathcal{Z} = \log \mathcal{N}(\mathbf{0}, \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I}) - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}). $$ This can be verified by applying simple rules for marginalizing Gaussians. Again, refer to Appendix VI for complete derivations. Refer to Appendix VII for a numerically efficient and robust method for computing these quantities.
Non-Gaussian Likelihoods
Recall from earlier that the ELBO is written as $$ \begin{align*} \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}) & = \int \log{\left(\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}\right)} q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \\ & = \int \left(\log{\Phi(\mathbf{y}, \mathbf{u})} + \log{\frac{p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}}\ \right) q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \\ & = \mathrm{ELL}(\boldsymbol{\phi}, \mathbf{Z}) - \mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{u})\|p(\mathbf{u})], \end{align*} $$ where we define $\mathrm{ELL}(\boldsymbol{\phi}, \mathbf{Z})$, the expected log-likelihood (ELL), as $$ \mathrm{ELL}(\boldsymbol{\phi}, \mathbf{Z}) \triangleq \mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{u})}\left[\log{\Phi(\mathbf{y}, \mathbf{u})}\right]. $$ This constitutes the first term in the ELBO, and can be written as $$ \begin{align*} \mathrm{ELL}(\boldsymbol{\phi}, \mathbf{Z}) & = \int \log{\Phi(\mathbf{y}, \mathbf{u})} q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \\ & = \int \left(\int \log{p(\mathbf{y} | \mathbf{f})} p(\mathbf{f} | \mathbf{u}) \,\mathrm{d}\mathbf{f}\right) q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \\ & = \int \log{p(\mathbf{y} | \mathbf{f})} \left(\int p(\mathbf{f} | \mathbf{u}) q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \right) \,\mathrm{d}\mathbf{f} \\ & = \int \log{p(\mathbf{y} | \mathbf{f})} q(\mathbf{f}) \,\mathrm{d}\mathbf{f} \\ & = \mathbb{E}_{q(\mathbf{f})}[\log{p(\mathbf{y} | \mathbf{f})}]. \end{align*} $$ While this integral is analytically intractable in general, we can nonetheless approximate it efficiently using numerical integration techniques such as Monte Carlo (MC) estimation or quadrature rules. In particular, because $q(\mathbf{f})$ is Gaussian, we can utilize simple yet effective rules such as Gauss-Hermite quadrature.
Now, the second term in the ELBO is the KL divergence between $q_{\boldsymbol{\phi}}(\mathbf{u})$ and $p(\mathbf{u})$, which are both multivariate Gaussians, $$ \mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{u})\|p(\mathbf{u})] = \mathrm{KL}[\mathcal{N}(\mathbf{b}, \mathbf{W} {\mathbf{W}}^\top) || \mathcal{N}(\mathbf{0}, \mathbf{K}_\mathbf{uu})], $$ and has a closed-form expression. In the case of the whitened parameterization, it can be simplified as $$ \begin{align*} \mathrm{KL}[q_{\boldsymbol{\phi}}(\mathbf{u})\|p(\mathbf{u})] & = \mathrm{KL}[\mathcal{N}(\mathbf{b}’, \mathbf{W}’ {\mathbf{W}’}^\top) || \mathcal{N}(\mathbf{0}, \mathbf{K}_\mathbf{uu})] \\ & = \mathrm{KL}[\mathcal{N}(\mathbf{b}, \mathbf{W} {\mathbf{W}}^\top) || \mathcal{N}(\mathbf{0}, \mathbf{I})]. \end{align*} $$ This comes from the fact that $$ \mathrm{KL}\left[\mathcal{N}(\mathbf{A} \boldsymbol{\mu}_0, \mathbf{A} \boldsymbol{\Sigma}_0 \mathbf{A}^\top) || \mathcal{N}(\mathbf{A} \boldsymbol{\mu}_1, \mathbf{A} \boldsymbol{\Sigma}_1 \mathbf{A}^\top) \right] = \mathrm{KL}\left[\mathcal{N}(\boldsymbol{\mu}_0, \boldsymbol{\Sigma}_0) || \mathcal{N}(\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) \right] $$ where we set $\boldsymbol{\mu}_0 = \mathbf{b}, \boldsymbol{\Sigma}_0 = \mathbf{W} \mathbf{W}^\top, \boldsymbol{\mu}_1 = \mathbf{0}, \boldsymbol{\Sigma}_1 = \mathbf{I}$ and $\mathbf{A} = \mathbf{L}$ where $\mathbf{L}$ is the Cholesky factor of $\mathbf{K}_\mathbf{uu}$, i.e. the lower triangular matrix such that $\mathbf{L}\mathbf{L}^\top = \mathbf{K}_\mathbf{uu}$.
Large-Scale Data with Stochastic Optimization
Links and Further Readings
- Papers:
- Forerunners: Deterministic Training Conditional (DTC; Csató & Opper, 20024; Seeger, 20035); Fully Independent Training Conditional (FITC; Snelson & Ghahramani, 20056; Quinonero-Candela & Rasmussen, 20057)
- Inter-domain Gaussian processes: Lázaro-Gredilla & Figueiras-Vidal, 20098
- Deep Gaussian processes: Damianou & Lawrence, 20139, Salimbeni et al, 201710
- Non-Gaussian likelihoods: Hensman et al, 201311; Dezfouli & Bonilla, 201512
- Unifying inducing-/pseudo-point approximations: Bui et al, 201713
- Orthogonal decompositions: Salimbeni et al, 201814; Shi et al, 202015
- Convergence analysis: Burt et al, 201916
- Efficient sampling: Wilson et al, 202017
- Technical Reports:
- Notes:
- Blog posts:
- Sparse GPs: approximate the posterior, not the model by J. Hensman
Cite as:
@article{tiao2020svgp,
title = "{A} {H}andbook for {S}parse {V}ariational {G}aussian {P}rocesses",
author = "Tiao, Louis C",
journal = "tiao.io",
year = "2020",
url = "https://tiao.io/post/sparse-variational-gaussian-processes/"
}
To receive updates on more posts like this, follow me on Twitter and GitHub!
Appendix
I
Whitened parameterization
Recall the definition $\boldsymbol{\Lambda} \triangleq \mathbf{L}^\top \boldsymbol{\Psi}$. Then, the mean simplifies to $$ \boldsymbol{\mu} = \boldsymbol{\Psi}^\top \mathbf{b} = \boldsymbol{\Psi}^\top (\mathbf{L} \mathbf{b}’) = (\mathbf{L}^\top \boldsymbol{\Psi})^\top \mathbf{b}’ = \boldsymbol{\Lambda}^\top \mathbf{b}’. $$ Similarly, the covariance simplifies to $$ \begin{align*} \mathbf{\Sigma} & = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^{\top} (\mathbf{K}_\mathbf{uu} - \mathbf{W} \mathbf{W}^{\top}) \boldsymbol{\Psi} \newline & = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^{\top} (\mathbf{L} \mathbf{L}^{\top} - \mathbf{L} ({\mathbf{W}’}{\mathbf{W}’}^{\top}) \mathbf{L}^{\top}) \boldsymbol{\Psi} \newline & = \mathbf{K}_\mathbf{ff} - (\mathbf{L}^{\top} \boldsymbol{\Psi})^{\top} ( \mathbf{I}_M - {\mathbf{W}’}{\mathbf{W}’}^{\top}) (\mathbf{L}^{\top} \boldsymbol{\Psi}) \newline & = \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^{\top} ( \mathbf{I}_M - {\mathbf{W}’}{\mathbf{W}’}^{\top}) \boldsymbol{\Lambda}. \end{align*} $$
II
SVGP Implementation Details
Single input index point
Here is an efficient and numerically stable way to compute $q_{\boldsymbol{\phi}}(f(\mathbf{x}))$ for an input $\mathbf{x}$. We take the following steps:
Cholesky decomposition: $\mathbf{L} \triangleq \mathrm{cholesky}(\mathbf{K}_\textbf{uu})$
Note: $\mathcal{O}(M^3)$ complexity.
Solve system of linear equations: $\boldsymbol{\lambda}(\mathbf{x}) \triangleq \mathbf{L} \backslash \mathbf{k}_\mathbf{u}(\mathbf{x})$
Note: $\mathcal{O}(M^2)$ complexity since $\mathbf{L}$ is lower triangular; $\boldsymbol{\beta} = \mathbf{A} \backslash \mathbf{x}$ denotes the vector $\boldsymbol{\beta}$ such that $\mathbf{A} \boldsymbol{\beta} = \mathbf{x} \Leftrightarrow \boldsymbol{\beta} = \mathbf{A}^{-1} \mathbf{x}$. Hence, $\boldsymbol{\lambda}(\mathbf{x}) = \mathbf{L}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x})$.
$s(\mathbf{x}, \mathbf{x}) \triangleq k_{\theta}(\mathbf{x}, \mathbf{x}) - \boldsymbol{\lambda}^\top(\mathbf{x}) \boldsymbol{\lambda}(\mathbf{x})$
Note: $$ \boldsymbol{\lambda}^\top(\mathbf{x}) \boldsymbol{\lambda}(\mathbf{x}) = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{L}^{-\top} \mathbf{L}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}) = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}) = \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu} \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}). $$
For whitened parameterization:
$\mu \triangleq \boldsymbol{\lambda}^\top(\mathbf{x}) \mathbf{b}'$
$\mathbf{v}^\top(\mathbf{x}) \triangleq \boldsymbol{\lambda}^\top(\mathbf{x}) {\mathbf{W}’}$
Note: $\mathbf{v}^\top(\mathbf{x}) \mathbf{v}(\mathbf{x}) = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{L}^{-\top} ({\mathbf{W}’} {\mathbf{W}’}^{\top}) \mathbf{L}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x})$
otherwise:
Solve system of linear equations: $\boldsymbol{\psi}_\mathbf{u}(\mathbf{x}) \triangleq \mathbf{L}^\top \backslash \boldsymbol{\lambda}(\mathbf{x})$
Note: $\mathcal{O}(M^2)$ complexity since $\mathbf{L}^{\top}$ is upper triangular. Further, $$ \boldsymbol{\psi}_\mathbf{u}(\mathbf{x}) = \mathbf{L}^{-\top} \boldsymbol{\lambda}(\mathbf{x}) = \mathbf{L}^{-\top} \mathbf{L}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}) = \mathbf{K}_\mathbf{uu}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x}) $$ and $$ \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu}^{-\top} = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu}^{-1} $$ since $\mathbf{K}_\mathbf{uu}$ is symmetric and nonsingular.
$\mu(\mathbf{x}) \triangleq \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{b}$
$\mathbf{v}^\top(\mathbf{x}) \triangleq \boldsymbol{\psi}_\mathbf{u}^\top(\mathbf{x}) \mathbf{W}$
Note: $\mathbf{v}^\top(\mathbf{x}) \mathbf{v}(\mathbf{x}) = \mathbf{k}_\mathbf{u}^\top(\mathbf{x}) \mathbf{K}_\mathbf{uu}^{-1} (\mathbf{W} \mathbf{W}^{\top}) \mathbf{K}_\mathbf{uu}^{-1} \mathbf{k}_\mathbf{u}(\mathbf{x})$
$\sigma^2(\mathbf{x}) \triangleq s(\mathbf{x}, \mathbf{x}) + \mathbf{v}^\top(\mathbf{x}) \mathbf{v}(\mathbf{x})$
Return $\mathcal{N}(f(\mathbf{x}) ; \mu(\mathbf{x}), \sigma^2(\mathbf{x}))$
Multiple input index points
It is simple to extend this to compute $q_{\boldsymbol{\phi}}(\mathbf{f})$ for an arbitary number of index points $\mathbf{X}$:
Cholesky decomposition: $\mathbf{L} = \mathrm{cholesky}(\mathbf{K}_\textbf{uu})$
Note: $\mathcal{O}(M^3)$ complexity.
Solve system of linear equations: $\boldsymbol{\Lambda} = \mathbf{L} \backslash \mathbf{K}_\mathbf{uf}$
Note: $\mathcal{O}(M^2)$ complexity since $\mathbf{L}$ is lower triangular; $\mathbf{B} = \mathbf{A} \backslash \mathbf{X}$ denotes the matrix $\mathbf{B}$ such that $\mathbf{A} \mathbf{B} = \mathbf{X} \Leftrightarrow \mathbf{B} = \mathbf{A}^{-1} \mathbf{X}$. Hence, $\boldsymbol{\Lambda} = \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf}$.
$\mathbf{S} \triangleq \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^{\top} \boldsymbol{\Lambda}$
Note: $$ \boldsymbol{\Lambda}^{\top} \boldsymbol{\Lambda} = \mathbf{K}_\mathbf{fu} \mathbf{L}^{-\top} \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf} = \mathbf{K}_\mathbf{fu} \mathbf{K}_\textbf{uu}^{-1} \mathbf{K}_\mathbf{uf} = \mathbf{K}_\mathbf{fu} \mathbf{K}_\textbf{uu}^{-1} (\mathbf{K}_\textbf{uu}) \mathbf{K}_\textbf{uu}^{-1} \mathbf{K}_\mathbf{uf} = \boldsymbol{\Psi}^\top \mathbf{K}_\textbf{uu} \boldsymbol{\Psi}. $$
For whitened parameterization:
$\boldsymbol{\mu} \triangleq \boldsymbol{\Lambda}^\top \mathbf{b}'$
$\mathbf{V}^\top \triangleq \boldsymbol{\Lambda}^\top {\mathbf{W}’}$
Note: $\mathbf{V}^\top \mathbf{V} = \mathbf{K}_\mathbf{fu} \mathbf{L}^{-\top} ({\mathbf{W}’} {\mathbf{W}’}^{\top}) \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf}.$
otherwise:
Solve system of linear equations: $\boldsymbol{\Psi} = \mathbf{L}^{\top} \backslash \boldsymbol{\Lambda}$
Note: $\mathcal{O}(M^2)$ complexity since $\mathbf{L}^{\top}$ is upper triangular. Further,
$$ \boldsymbol{\Psi} = \mathbf{L}^{-\top} \boldsymbol{\Lambda} = \mathbf{L}^{-\top} \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf} = (\mathbf{L}\mathbf{L}^\top)^{-1} \mathbf{K}_\mathbf{uf} = \mathbf{K}_\mathbf{uu}^{-1} \mathbf{K}_\mathbf{uf}, $$ and $$ \boldsymbol{\Psi}^\top = \mathbf{K}_\mathbf{fu} \mathbf{K}_\mathbf{uu}^{-\top} = \mathbf{K}_\mathbf{fu} \mathbf{K}_\mathbf{uu}^{-1}, $$ since $\mathbf{K}_\mathbf{uu}$ is symmetric and nonsingular.
$\boldsymbol{\mu} \triangleq \boldsymbol{\Psi}^\top \mathbf{b}$
$\mathbf{V}^\top \triangleq \boldsymbol{\Psi}^\top \mathbf{W}$
Note: $\mathbf{V}^\top \mathbf{V} = \mathbf{K}_\mathbf{fu} \mathbf{K}_\mathbf{uu}^{-1} (\mathbf{W} \mathbf{W}^{\top}) \mathbf{K}_\mathbf{uu}^{-1} \mathbf{K}_\mathbf{uf}$.
$\mathbf{\Sigma} \triangleq \mathbf{S} + \mathbf{V}^\top \mathbf{V}$
Return $\mathcal{N}(\mathbf{f} ; \boldsymbol{\mu}, \mathbf{\Sigma})$
In TensorFlow, this looks something like:
import tensorflow as tf
def variational_predictive(Knn, Kmm, Kmn, W, b, whiten=True, jitter=1e-6):
L = tf.linalg.cholesky(Kmm + jitter * tf.eye(m)) # L L^T = Kmm + jitter I_m
Lambda = tf.linalg.triangular_solve(L, Kmn, lower=True) # Lambda = L^{-1} Kmn
S = Knn - tf.linalg.matmul(Lambda, Lambda, adjoint_a=True) # Knn - Lambda^T Lambda
# Phi = L^{-T} L^{-1} Kmn = Kmm^{-1} Kmn
Phi = Lambda if whiten else tf.linalg.triangular_solve(L, Lambda, adjoint=True, lower=True)
U = tf.linalg.matmul(Phi, W, adjoint_a=True) # U = V^T = Phi^T W
mu = tf.linalg.matmul(Phi, b, adjoint_a=True) # Phi^T b
Sigma = S + tf.linalg.matmul(U, U, adjoint_b=True) # S + UU^T = S + V^T V
return mu, Sigma
III
Optimal variational distribution (in general)
Taking the functional derivative of the ELBO wrt to $q_{\boldsymbol{\phi}}(\mathbf{u})$, we get $$ \begin{align*} \frac{\partial}{\partial q_{\boldsymbol{\phi}}(\mathbf{u})} \mathrm{ELBO}(\boldsymbol{\phi}, \mathbf{Z}) & = \frac{\partial}{\partial q_{\boldsymbol{\phi}}(\mathbf{u})} \left ( \int \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} q_{\boldsymbol{\phi}}(\mathbf{u}) \,\mathrm{d}\mathbf{u} \right ) \newline & = \int \frac{\partial}{\partial q_{\boldsymbol{\phi}}(\mathbf{u})} \left ( \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} q_{\boldsymbol{\phi}}(\mathbf{u}) \right ) \,\mathrm{d}\mathbf{u} \newline & = \begin{split} & \int \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} \left ( \frac{\partial}{\partial q_{\boldsymbol{\phi}}(\mathbf{u})} q_{\boldsymbol{\phi}}(\mathbf{u}) \right ) + \newline & \qquad q_{\boldsymbol{\phi}}(\mathbf{u}) \left ( \frac{\partial}{\partial q_{\boldsymbol{\phi}}(\mathbf{u})} \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} \right ) \,\mathrm{d}\mathbf{u} \end{split} \newline & = \int \log{\frac{\Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u})}{q_{\boldsymbol{\phi}}(\mathbf{u})}} + q_{\boldsymbol{\phi}}(\mathbf{u}) \left ( -\frac{1}{q_{\boldsymbol{\phi}}(\mathbf{u})} \right ) \,\mathrm{d}\mathbf{u} \newline & = \int \log{\Phi(\mathbf{y}, \mathbf{u})} + \log{p(\mathbf{u})} - \log{q_{\boldsymbol{\phi}}(\mathbf{u})} - 1 \,\mathrm{d}\mathbf{u}. \end{align*} $$ Setting this expression to zero, we have $$ \begin{align*} \log{q_{\boldsymbol{\phi}^{\star}}(\mathbf{u})} & = \log{\Phi(\mathbf{y}, \mathbf{u})} + \log{p(\mathbf{u})} - 1 \\ \Rightarrow \qquad q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) & \propto \Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u}). \end{align*} $$
IV
Variational lower bound (partial) for Gaussian likelihoods
To carry out this derivation, we will need to recall the following two simple
identities. First, we can write the inner product between two vectors as the
trace of their outer product,
$$
\mathbf{a}^\top \mathbf{b} = \mathrm{tr}(\mathbf{a} \mathbf{b}^\top).
$$
Second, the relationship between the auto-correlation matrix $\mathbb{E}[\mathbf{a}\mathbf{a}^{\top}]$
and the covariance matrix,
$$
\begin{align*}
\mathrm{Cov}[\mathbf{a}] & = \mathbb{E}[\mathbf{a}\mathbf{a}^{\top}] - \mathbb{E}[\mathbf{a}] \, \mathbb{E}[\mathbf{a}]^\top \\
\Leftrightarrow \quad
\mathbb{E}[\mathbf{a}\mathbf{a}^{\top}] & = \mathrm{Cov}[\mathbf{a}] + \mathbb{E}[\mathbf{a}] \, \mathbb{E}[\mathbf{a}]^\top
\end{align*}
$$
These allow us to write
$$
\begin{align*}
\log{\Phi(\mathbf{y}, \mathbf{u})} & =
\int \log{\mathcal{N}(\mathbf{y} | \mathbf{f}, \beta^{-1} \mathbf{I})} \mathcal{N}(\mathbf{f} | \mathbf{m}, \mathbf{S}) \,\mathrm{d}\mathbf{f}
\newline & = - \frac{1}{2\sigma^2} \int (\mathbf{y} - \mathbf{f})^{\top} (\mathbf{y} - \mathbf{f}) \mathcal{N}(\mathbf{f} | \mathbf{m}, \mathbf{S}) \,\mathrm{d}\mathbf{f} - \frac{N}{2}\log{(2\pi\sigma^2)}
\newline & = - \frac{1}{2\sigma^2} \int \mathrm{tr} \left (\mathbf{y}\mathbf{y}^{\top} - 2 \mathbf{y}\mathbf{f}^{\top} + \mathbf{f}\mathbf{f}^{\top} \right) \mathcal{N}(\mathbf{f} | \mathbf{m}, \mathbf{S}) \,\mathrm{d}\mathbf{f} - \frac{N}{2}\log{(2\pi\sigma^2)}
\newline & = - \frac{1}{2\sigma^2} \mathrm{tr} \left (\mathbf{y}\mathbf{y}^{\top} - 2 \mathbf{y}\mathbf{m}^{\top} + \mathbf{S} + \mathbf{m} \mathbf{m}^{\top} \right) -
\frac{N}{2}\log{(2\pi\sigma^2)}
\newline & = - \frac{1}{2\sigma^2} (\mathbf{y} - \mathbf{m})^{\top} (\mathbf{y} - \mathbf{m}) - \frac{N}{2}\log{(2\pi\sigma^2)} - \frac{1}{2\sigma^2} \mathrm{tr}(\mathbf{S})
\newline & = \log{\mathcal{N}(\mathbf{y} | \mathbf{m}, \beta^{-1} \mathbf{I} )} - \frac{1}{2\sigma^2} \mathrm{tr}(\mathbf{S}).
\end{align*}
$$
V
Optimal variational distribution for Gaussian likelihoods
Firstly, the optimal variational distribution can be found in closed-form as $$ \begin{align*} q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) & \propto \Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u}) \\ & \propto \mathcal{N}(\mathbf{y} \mid \boldsymbol{\Psi}^\top \mathbf{u}, \beta^{-1} \mathbf{I}) \mathcal{N}(\mathbf{u} \mid \mathbf{0}, \mathbf{K}_\mathbf{uu}) \\ & \propto \exp \left ( - \frac{\beta}{2} (\mathbf{y} - \boldsymbol{\Psi}^\top \mathbf{u})^\top (\mathbf{y} - \boldsymbol{\Psi}^\top \mathbf{u}) - \frac{1}{2} \mathbf{u}^\top \mathbf{K}_\mathbf{uu}^{-1} \mathbf{u} \right ) \\ & \propto \exp \left ( - \frac{1}{2} \left ( \mathbf{u}^\top \mathbf{C} \mathbf{u} - 2 \beta (\boldsymbol{\Psi} \mathbf{y})^\top \mathbf{u} \right ) \right ), \end{align*} $$ where $$ \mathbf{C} \triangleq \mathbf{K}_\mathbf{uu}^{-1} + \beta \boldsymbol{\Psi} \boldsymbol{\Psi}^\top = \mathbf{K}_\mathbf{uu}^{-1} (\mathbf{K}_\mathbf{uu} + \beta \mathbf{K}_\mathbf{uf} \mathbf{K}_\mathbf{fu} ) \mathbf{K}_\mathbf{uu}^{-1}. $$ By completing the square, we get $$ \begin{align*} q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) & \propto \exp \left ( - \frac{1}{2} (\mathbf{u} - \beta \mathbf{C}^{-1} \boldsymbol{\Psi} \mathbf{y})^\top \mathbf{C} (\mathbf{u} - \beta \mathbf{C}^{-1} \boldsymbol{\Psi} \mathbf{y}) \right ) \\ & \propto \mathcal{N}(\mathbf{u} \mid \beta \mathbf{C}^{-1} \boldsymbol{\Psi} \mathbf{y}, \mathbf{C}^{-1}). \end{align*} $$ We define $$ \mathbf{M} \triangleq \mathbf{K}_\mathbf{uu} + \beta \mathbf{K}_\mathbf{uf} \mathbf{K}_\mathbf{fu} $$ so that $$ \mathbf{C} = \mathbf{K}_\mathbf{uu}^{-1} \mathbf{M} \mathbf{K}_\mathbf{uu}^{-1}, $$ which allows us to write $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) = \mathcal{N}(\mathbf{u} \mid \beta \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uf} \mathbf{y}, \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uu}). $$
VI
Variational lower bound (complete) for Gaussian likelihoods
We have
$$
\begin{align*}
\mathrm{ELBO}(\boldsymbol{\phi}^{\star}, \mathbf{Z}) & =
\log \mathcal{Z} \\ & =
\log \int \Phi(\mathbf{y}, \mathbf{u}) p(\mathbf{u}) \,\mathrm{d}\mathbf{u} \\ & =
\log \left [ \exp{\left(-\frac{\beta}{2} \mathrm{tr}(\mathbf{S})\right)} \int \mathcal{N}(\mathbf{y} | \boldsymbol{\Psi}^{\top} \mathbf{u}, \beta^{-1} \mathbf{I}) p(\mathbf{u}) \,\mathrm{d}\mathbf{u} \right ] \\ & =
\log \int \mathcal{N}(\mathbf{y} \mid \boldsymbol{\Psi}^{\top} \mathbf{u}, \beta^{-1} \mathbf{I}) \mathcal{N}(\mathbf{u} \mid \mathbf{0}, \mathbf{K}_\mathbf{uu}) \,\mathrm{d}\mathbf{u} - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}) \\ & =
\log \mathcal{N}(\mathbf{y} \mid \mathbf{0}, \beta^{-1} \mathbf{I} + \boldsymbol{\Psi}^{\top} \mathbf{K}_\textbf{uu} \boldsymbol{\Psi}) - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}) \\ & =
\log \mathcal{N}(\mathbf{y} \mid \mathbf{0}, \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I}) - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}).
\end{align*}
$$
VII
SGPR Implementation Details
Here we provide implementation details that simultaneously minimizes the computational demands while avoiding numerically unstable calculations.
The difficulty in calculating the ELBO stem from terms involving the inverse and the determinant of $\mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I}$. More specifically, we have $$ \begin{split} \mathrm{ELBO}(\boldsymbol{\phi}^{\star}, \mathbf{Z}) & = - \frac{1}{2} \left( \log \det \left ( \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I} \right ) + \mathbf{y}^\top \left ( \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I} \right )^{-1} \mathbf{y} + N \log {2\pi} \right) \\ & \qquad - \frac{\beta}{2} \mathrm{tr}(\mathbf{S}). \end{split} $$ It turns out that many of the required terms can be expressed in terms of the symmetric positive definite matrix $$ \mathbf{B} \triangleq \mathbf{U} \mathbf{U}^\top + \mathbf{I}, $$ where $\mathbf{U} \triangleq \beta^{\frac{1}{2}} \boldsymbol{\Lambda}$.
First, let’s tackle the inverse term. Using the Woodbury identity, we can write it as $$ \begin{align*} \left(\mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I}\right)^{-1} & = \left(\beta^{-1} \mathbf{I} + \boldsymbol{\Psi}^\top \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi}\right)^{-1} \\ & = \beta \mathbf{I} - \beta^2 \boldsymbol{\Psi}^\top \left(\mathbf{K}_\mathbf{uu}^{-1} + \beta \boldsymbol{\Psi} \boldsymbol{\Psi}^\top \right)^{-1} \boldsymbol{\Psi} \\ & = \beta \left(\mathbf{I} - \beta \boldsymbol{\Psi}^\top \mathbf{C}^{-1} \boldsymbol{\Psi}\right). \end{align*} $$
Recall that $\mathbf{C}^{-1} = \mathbf{K}_\mathbf{uu} \mathbf{M}^{-1} \mathbf{K}_\mathbf{uu}$. We can expand $\mathbf{M}$ as $$ \begin{align*} \mathbf{M} & \triangleq \mathbf{K}_\mathbf{uu} + \beta \mathbf{K}_\mathbf{uf} \mathbf{K}_\mathbf{fu} \\ & = \mathbf{L} \mathbf{L}^\top + \beta \mathbf{L} \mathbf{L}^{-1} \mathbf{K}_\mathbf{uf} \mathbf{K}_\mathbf{fu} \mathbf{L}^{-\top} \mathbf{L}^\top \\ & = \mathbf{L} \left( \mathbf{I} + \beta \boldsymbol{\Lambda} \boldsymbol{\Lambda}^\top \right) \mathbf{L}^\top \\ & = \mathbf{L} \mathbf{B} \mathbf{L}^{\top}, \end{align*} $$ so its inverse is simply $$ \mathbf{M}^{-1} = \mathbf{L}^{-\top} \mathbf{B}^{-1} \mathbf{L}^{-1}. $$ Therefore, we have $$ \begin{align*} \mathbf{C}^{-1} & = \mathbf{K}_\mathbf{uu} \mathbf{L}^{-\top} \mathbf{B}^{-1} \mathbf{L}^{-1} \mathbf{K}_\mathbf{uu} \\ & = \mathbf{L} \mathbf{B}^{-1} \mathbf{L}^\top \\ & = \mathbf{W} \mathbf{W}^\top \end{align*} $$ where $$ \mathbf{W} \triangleq \mathbf{L} \mathbf{L}_\mathbf{B}^{-\top} $$ and $\mathbf{L}_\mathbf{B}$ is the Cholesky factor of $\mathbf{B}$, i.e. the lower triangular matrix such that $\mathbf{L}_\mathbf{B}\mathbf{L}_\mathbf{B}^\top = \mathbf{B}$. All in all, we now have $$ \begin{align*} \left(\mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I}\right)^{-1} & = \beta \left(\mathbf{I} - \beta \boldsymbol{\Psi}^\top \mathbf{W} \mathbf{W}^\top \boldsymbol{\Psi}\right), \end{align*} $$ so we can compute the quadratic term in $\mathbf{y}$ as $$ \begin{align*} \mathbf{y}^\top \left ( \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I} \right )^{-1} \mathbf{y} & = \beta \left( \mathbf{y}^\top \mathbf{y} - \beta \mathbf{y}^\top \boldsymbol{\Psi}^\top \mathbf{W} \mathbf{W}^\top \boldsymbol{\Psi} \mathbf{y} \right) \\ & = \beta \mathbf{y}^\top \mathbf{y} - \mathbf{c}^\top \mathbf{c}, \end{align*} $$ where $$ \mathbf{c} \triangleq \beta \mathbf{W}^\top \boldsymbol{\Psi} \mathbf{y} = \beta \mathbf{L}_\mathbf{B}^{-1} \boldsymbol{\Lambda} \mathbf{y} = \beta^{\frac{1}{2}} \mathbf{L}_\mathbf{B}^{-1} \mathbf{U} \mathbf{y}. $$
Next, let’s address the determinant term. To this end, first note that the determinant of $\mathbf{M}$ is $$ \begin{align*} \det \left( \mathbf{M} \right) & = \det \left( \mathbf{L} \mathbf{B} \mathbf{L}^{\top} \right) \\ & = \det \left( \mathbf{L} \right) \det \left( \mathbf{B} \right) \det \left( \mathbf{L}^{\top} \right) \\ & = \det \left( \mathbf{K}_\mathbf{uu} \right) \det \left( \mathbf{B} \right). \end{align*} $$ Hence, the determinant of $\mathbf{C}$ is $$ \begin{align*} \det \left( \mathbf{C} \right) & = \det \left( \mathbf{K}_\mathbf{uu}^{-1} \mathbf{M} \mathbf{K}_\mathbf{uu}^{-1} \right) \\ & = \frac{\det \left( \mathbf{M} \right)}{\det \left( \mathbf{K}_\mathbf{uu} \right )^2} \\ & = \frac{\det \left( \mathbf{B} \right)}{\det \left( \mathbf{K}_\mathbf{uu} \right )}. \end{align*} $$ Therefore, by the matrix determinant lemma, we have $$ \begin{align*} \det \left( \mathbf{Q}_\mathbf{ff} + \beta^{-1} \mathbf{I} \right) & = \det \left( \beta^{-1} \mathbf{I} + \boldsymbol{\Psi}^\top \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi} \right) \\ & = \det \left( \mathbf{K}_\mathbf{uu}^{-1} + \beta \boldsymbol{\Psi} \boldsymbol{\Psi}^\top \right) \det \left( \mathbf{K}_\mathbf{uu} \right) \det \left( \beta^{-1} \mathbf{I} \right) \\ & = \det \left( \mathbf{C} \right) \det \left( \mathbf{K}_\mathbf{uu} \right) \det \left( \beta^{-1} \mathbf{I} \right) \\ & = \det \left( \mathbf{B} \right) \det \left( \beta^{-1} \mathbf{I} \right). \end{align*} $$ We can re-use $\mathbf{L}_\mathbf{B}$ to calculate $\det \left( \mathbf{B} \right)$ in linear time.
The last non-trivial component of the ELBO is the trace term, which can be calculated as $$ \frac{\beta}{2} \mathrm{tr}(\mathbf{S}) = \frac{\beta}{2} \mathrm{tr}\left(\mathbf{K}_\mathbf{ff}\right) - \frac{1}{2} \mathrm{tr}\left(\mathbf{U} \mathbf{U}^\top \right), $$ since $$ \begin{align*} \mathrm{tr}\left(\mathbf{U} \mathbf{U}^\top\right) & = \mathrm{tr}\left(\mathbf{U}^\top \mathbf{U}\right) \\ & = \beta \cdot \mathrm{tr}\left(\boldsymbol{\Lambda} \boldsymbol{\Lambda}^\top\right) \\ & = \beta \cdot \mathrm{tr}\left( \boldsymbol{\Psi}^{\top} \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi} \right). \end{align*} $$ Again, we can re-use $\mathbf{U} \mathbf{U}^\top$ computed earlier.
Finally, let us address the posterior predictive. Recall that $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) = \mathcal{N}(\mathbf{u} \mid \beta \mathbf{C}^{-1} \boldsymbol{\Psi} \mathbf{y}, \mathbf{C}^{-1}). $$ Re-writing this in terms of $\mathbf{W}$, we get $$ \begin{align*} q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) & = \mathcal{N}\left(\mathbf{u} \mid \beta \mathbf{W} \mathbf{W}^\top \boldsymbol{\Psi} \mathbf{y}, \mathbf{W} \mathbf{W}^\top \right) \\ & = \mathcal{N}\left(\mathbf{u} \mid \beta \mathbf{L} \mathbf{L}_\mathbf{B}^{-\top} \mathbf{W}^\top \boldsymbol{\Psi} \mathbf{y}, \mathbf{L} \mathbf{L}_\mathbf{B}^{-\top} \mathbf{L}_\mathbf{B}^{-1} \mathbf{L}^\top\right) \\ & = \mathcal{N}\left(\mathbf{u} \mid \mathbf{L} \left(\mathbf{L}_\mathbf{B}^{-\top} \mathbf{c}\right), \mathbf{L} \mathbf{B}^{-1} \mathbf{L}^\top\right). \end{align*} $$ Hence, we see that the optimal variational distribution is itself a whitened parameterization with $\mathbf{b}’ = \mathbf{L}_\mathbf{B}^{-\top} \mathbf{c}$ and $\mathbf{W}’ = \mathbf{L}_\mathbf{B}^{-\top}$ (such that ${\mathbf{W}’} {\mathbf{W}’}^\top = \mathbf{B}^{-1}$). Combined with results from a previous section, we can directly write the predictive $q_{\boldsymbol{\phi}^{\star}}(\mathbf{f}) = \int p(\mathbf{f}|\mathbf{u}) q_{\boldsymbol{\phi}^{\star}}(\mathbf{u}) \, \mathrm{d}\mathbf{u}$ as $$ q_{\boldsymbol{\phi}^{\star}}(\mathbf{f}) = \mathcal{N}\left(\boldsymbol{\Lambda}^\top \mathbf{L}_\mathbf{B}^{-\top} \mathbf{c}, \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^\top \left( \mathbf{I} - \mathbf{B}^{-1} \right) \boldsymbol{\Lambda} \right). $$ Alternatively, we can derive this by noting the following simple identity, $$ \boldsymbol{\Psi}^\top \mathbf{C}^{-1} \boldsymbol{\Psi} = \boldsymbol{\Psi}^\top \mathbf{L} \mathbf{B}^{-1} \mathbf{L}^\top \boldsymbol{\Psi} = \boldsymbol{\Lambda}^\top \mathbf{B}^{-1} \boldsymbol{\Lambda}, $$ and applying the rules for marginalizing Gaussians to obtain $$ \begin{align*} q_{\boldsymbol{\phi}^{\star}}(\mathbf{f}) & = \mathcal{N}\left(\beta \boldsymbol{\Psi}^\top \mathbf{C}^{-1} \boldsymbol{\Psi} \mathbf{y}, \mathbf{K}_\mathbf{ff} - \boldsymbol{\Psi}^\top \mathbf{K}_\mathbf{uu} \boldsymbol{\Psi} + \boldsymbol{\Psi}^\top \mathbf{C}^{-1} \boldsymbol{\Psi} \right) \\ & = \mathcal{N}\left(\beta \boldsymbol{\Lambda}^\top \mathbf{B}^{-1} \boldsymbol{\Lambda} \mathbf{y}, \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^\top \boldsymbol{\Lambda} + \boldsymbol{\Lambda}^\top \mathbf{B}^{-1} \boldsymbol{\Lambda} \right) \\ & = \mathcal{N}\left(\boldsymbol{\Lambda}^\top \mathbf{L}_\mathbf{B}^{-\top} \mathbf{c}, \mathbf{K}_\mathbf{ff} - \boldsymbol{\Lambda}^\top \left( \mathbf{I} - \mathbf{B}^{-1} \right) \boldsymbol{\Lambda} \right). \end{align*} $$
Titsias, M. (2009, April). Variational Learning of Inducing Variables in Sparse Gaussian Processes. In Artificial Intelligence and Statistics (pp. 567-574). ↩︎
Murray, I., & Adams, R. P. (2010). Slice Sampling Covariance Hyperparameters of Latent Gaussian Models. In Advances in Neural Information Processing Systems (pp. 1732-1740). ↩︎
Hensman, J., Matthews, A. G., Filippone, M., & Ghahramani, Z. (2015). MCMC for Variationally Sparse Gaussian Processes. In Advances in Neural Information Processing Systems (pp. 1648-1656). ↩︎
Csató, L., & Opper, M. (2002). Sparse On-line Gaussian Processes. Neural Computation, 14(3), 641-668. ↩︎
Seeger, M. (2003). Bayesian Gaussian Process Models: PAC-Bayesian Generalisation Error Bounds and Sparse Approximations (PhD Thesis). University of Edinburgh. ↩︎
Snelson, E., & Ghahramani, Z. (2005). Sparse Gaussian Processes using Pseudo-inputs. Advances in Neural Information Processing Systems, 18, 1257-1264. ↩︎
Quinonero-Candela, J., & Rasmussen, C. E. (2005). A Unifying View of Sparse Approximate Gaussian Process Regression. The Journal of Machine Learning Research, 6, 1939-1959. ↩︎
Lázaro-Gredilla, M., & Figueiras-Vidal, A. R. (2009, December). Inter-domain Gaussian Processes for Sparse Inference using Inducing Features. In Advances in Neural Information Processing Systems. ↩︎
Damianou, A., & Lawrence, N. D. (2013, April). Deep Gaussian Processes. In Artificial Intelligence and Statistics (pp. 207-215). PMLR. ↩︎
Salimbeni, H., & Deisenroth, M. (2017). Doubly Stochastic Variational Inference for Deep Gaussian Processes. Advances in Neural Information Processing Systems, 30. ↩︎
Hensman, J., Fusi, N., & Lawrence, N. D. (2013, August). Gaussian Processes for Big Data. In Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence (pp. 282-290). ↩︎
Dezfouli, A., & Bonilla, E. V. (2015). Scalable Inference for Gaussian Process Models with Black-box Likelihoods. In Advances in Neural Information Processing Systems (pp. 1414-1422). ↩︎
Bui, T. D., Yan, J., & Turner, R. E. (2017). A Unifying Framework for Gaussian Process Pseudo-point Approximations using Power Expectation Propagation. The Journal of Machine Learning Research, 18(1), 3649-3720. ↩︎
Salimbeni, H., Cheng, C. A., Boots, B., & Deisenroth, M. (2018). Orthogonally Decoupled Variational Gaussian Processes. In Advances in Neural Information Processing Systems (pp. 8711-8720). ↩︎
Shi, J., Titsias, M., & Mnih, A. (2020, June). Sparse Orthogonal Variational Inference for Gaussian Processes. In International Conference on Artificial Intelligence and Statistics (pp. 1932-1942). PMLR. ↩︎
Burt, D., Rasmussen, C. E., & Van Der Wilk, M. (2019, May). Rates of Convergence for Sparse Variational Gaussian Process Regression. In International Conference on Machine Learning (pp. 862-871). PMLR. ↩︎
Wilson, J., Borovitskiy, V., Terenin, A., Mostowsky, P., & Deisenroth, M. (2020, November). Efficiently Sampling Functions from Gaussian Process Posteriors. In International Conference on Machine Learning (pp. 10292-10302). PMLR. ↩︎