A Tutorial on Variational Autoencoders with a Concise Keras Implementation
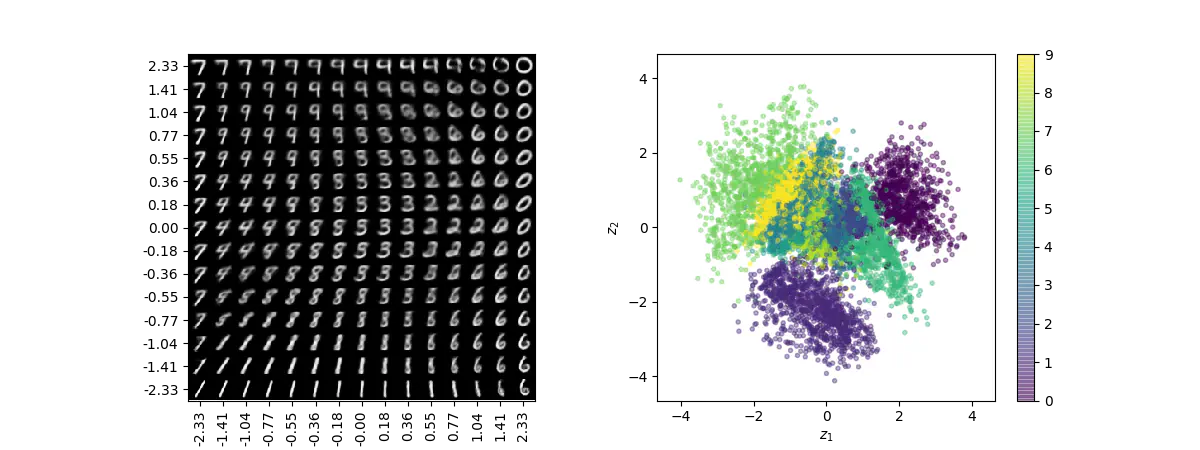 Visualization of 2D manifold of MNIST digits (left) and the representation of digits in latent space colored according to their digit labels (right).
Visualization of 2D manifold of MNIST digits (left) and the representation of digits in latent space colored according to their digit labels (right).Keras is awesome. It is a very well-designed library that clearly abides by its guiding principles of modularity and extensibility, enabling us to easily assemble powerful, complex models from primitive building blocks. This has been demonstrated in numerous blog posts and tutorials, in particular, the excellent tutorial on Building Autoencoders in Keras. As the name suggests, that tutorial provides examples of how to implement various kinds of autoencoders in Keras, including the variational autoencoder (VAE)1.
Like all autoencoders, the variational autoencoder is primarily used for unsupervised learning of hidden representations. However, they are fundamentally different to your usual neural network-based autoencoder in that they approach the problem from a probabilistic perspective. They specify a joint distribution over the observed and latent variables, and approximate the intractable posterior conditional density over latent variables with variational inference, using an inference network 2 3 (or more classically, a recognition model 4) to amortize the cost of inference.
While the examples in the aforementioned tutorial do well to showcase the versatility of Keras on a wide range of autoencoder model architectures, its implementation of the variational autoencoder doesn’t properly take advantage of Keras’ modular design, making it difficult to generalize and extend in important ways. As we will see, it relies on implementing custom layers and constructs that are restricted to a specific instance of variational autoencoders. This is a shame because when combined, Keras’ building blocks are powerful enough to encapsulate most variants of the variational autoencoder and more generally, recognition-generative model combinations for which the generative model belongs to a large family of deep latent Gaussian models (DLGMs)5.
The goal of this post is to propose a clean and elegant alternative implementation that takes better advantage of Keras’ modular design. It is not intended as tutorial on variational autoencoders 6. Rather, we study variational autoencoders as a special case of variational inference in deep latent Gaussian models using inference networks, and demonstrate how we can use Keras to implement them in a modular fashion such that they can be easily adapted to approximate inference in tasks beyond unsupervised learning, and with complicated (non-Gaussian) likelihoods.
This first post will lay the groundwork for a series of future posts that explore ways to extend this basic modular framework to implement the cutting-edge methods proposed in the latest research, such as the normalizing flows for building richer posterior approximations 7, importance weighted autoencoders 8, the Gumbel-softmax trick for inference in discrete latent variables 9, and even the most recent GAN-based density-ratio estimation techniques for likelihood-free inference 10 11.
Model specification
First, it is important to understand that the variational autoencoder is not a way to train generative models. Rather, the generative model is a component of the variational autoencoder and is, in general, a deep latent Gaussian model. In particular, let $\mathbf{x}$ be a local observed variable and $\mathbf{z}$ its corresponding local latent variable, with joint distribution
$$ p_{\theta}(\mathbf{x}, \mathbf{z}) = p_{\theta}(\mathbf{x} | \mathbf{z}) p(\mathbf{z}). $$
In Bayesian modelling, we assume the distribution of observed variables to be governed by the latent variables. Latent variables are drawn from a prior density $p(\mathbf{z})$ and related to the observations through the likelihood $p_{\theta}(\mathbf{x} | \mathbf{z})$. Deep latent Gaussian models (DLGMs) are a general class of models where the observed variable is governed by a hierarchy of latent variables, and the latent variables at each level of the hierarchy are Gaussian a priori 5.
In a typical instance of the variational autoencoder, we have only a single layer of latent variables with a Normal prior distribution,
$$ p(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I}). $$
Now, each local latent variable is related to its corresponding observation through the likelihood $p_{\theta}(\mathbf{x} | \mathbf{z})$, which can be viewed as a probabilistic decoder. Given a hidden lower-dimensional representation (or “code”) $\mathbf{z}$, it “decodes” it into a distribution over the observation $\mathbf{x}$.
Decoder
In this example, we define $p_{\theta}(\mathbf{x} | \mathbf{z})$ to be a multivariate Bernoulli whose probabilities are computed from $\mathbf{z}$ using a fully-connected neural network with a single hidden layer,
$$ \begin{align*} p_{\theta}(\mathbf{x} | \mathbf{z}) & = \mathrm{Bern}( \sigma( \mathbf{W}_2 \mathbf{h} + \mathbf{b}_2 ) ), \newline \mathbf{h} & = h(\mathbf{W}_1 \mathbf{z} + \mathbf{b}_1), \end{align*} $$
where $\sigma$ is the logistic sigmoid function, $h$ is some non-linearity, and the model parameters $\theta = \{ \mathbf{W}_1, \mathbf{W}_2, \mathbf{b}_1, \mathbf{b}_2 \}$ consist of the weights and biases of this neural network.
It is straightforward to implement this in Keras with the Sequential model API:
decoder = Sequential([
Dense(intermediate_dim, input_dim=latent_dim, activation='relu'),
Dense(original_dim, activation='sigmoid')
])
You can view a summary of the model parameters $\theta$ by calling
decoder.summary(). Additionally, you can produce a high-level diagram of
the network architecture, and optionally the input and output shapes of each
layer using plot_model from the
keras.utils.vis_utils module. Although our architecture is about as
simple as it gets, it is included in the figure below as an example of what
the diagrams look like.
Note that by fixing $\mathbf{W}_1$, $\mathbf{b}_1$ and $h$ to be the identity
matrix, the zero vector, and the identity function, respectively (or
equivalently dropping the first Dense layer in the snippet above
altogether), we recover logistic factor analysis.
With similarly minor modifications, we can recover other members from the
family of DLGMs, which include non-linear factor analysis,
non-linear Gaussian belief networks, sigmoid belief networks, and many
others 5.
Having specified how the probabilities are computed, we can now define the negative log likelihood of a Bernoulli $- \log p_{\theta}(\mathbf{x}|\mathbf{z})$, which is in fact equivalent to the binary cross-entropy loss:
def nll(y_true, y_pred):
""" Negative log likelihood (Bernoulli). """
# keras.losses.binary_crossentropy gives the mean
# over the last axis. we require the sum
return K.sum(K.binary_crossentropy(y_true, y_pred), axis=-1)
As we discuss later, this will not be the loss we ultimately minimize, but will constitute the data-fitting term of our final loss.
Note this is a valid definition of a Keras loss,
which is required to compile and optimize a model. It is a symbolic function
that returns a scalar for each data-point in y_true and y_pred.
In our example, y_pred will be the output of our decoder network, which
are the predicted probabilities, and y_true will be the true probabilities.
Side note: Using TensorFlow Distributions in loss
If you are using the TensorFlow backend, you can directly use the (negative)
log probability of Bernoulli from TensorFlow Distributions as a Keras
loss, as I demonstrate in my post on
Using negative log-likelihoods of TensorFlow Distributions as Keras losses.
Specifically we can define the loss as,
def nll(y_true, y_pred):
""" Negative log likelihood (Bernoulli). """
lh = K.tf.distributions.Bernoulli(probs=y_pred)
return - K.sum(lh.log_prob(y_true), axis=-1)
This is exactly equivalent to the previous definition, but does not call
K.binary_crossentropy directly.
Inference
Having specified the generative process, we would now like to perform inference on the latent variables and model parameters $\mathbf{z}$ and $\theta$, respectively. In particular, our goal is to compute the posterior $p_{\theta}(\mathbf{z} | \mathbf{x})$, the conditional density of the latent variable $\mathbf{z}$ given observed variable $\mathbf{x}$. Additionally, we wish to optimize the model parameters $\theta$ with respect to the marginal likelihood $p_{\theta}(\mathbf{x})$. Both depend on the marginal likelihood, whose calculation requires marginalizing out the latent variables $\mathbf{z}$. In general, this is computational intractable, requiring exponential time to compute, or it is analytically intractable and cannot be evaluated in closed-form. In our case, we suffer from the latter intractability, since our prior is Gaussian non-conjugate to the Bernoulli likelihood.
To circumvent this intractability we turn to variational inference, which formulates inference as an optimization problem. It seeks an approximate posterior $q_{\phi}(\mathbf{z} | \mathbf{x})$ closest in Kullback-Leibler (KL) divergence to the true posterior. More precisely, the approximate posterior is parameterized by variational parameters $\phi$, and we seek a setting of these parameters that minimizes the aforementioned KL divergence,
$$ \phi^* = \mathrm{argmin}_{\phi} \mathrm{KL} [q_{\phi}(\mathbf{z} | \mathbf{x}) || p_{\theta}(\mathbf{z} | \mathbf{x}) ] $$
With the luck we’ve had so far, it shouldn’t come as a surprise anymore that this too is intractable. It also depends on the log marginal likelihood, whose intractability is the reason we appealed to approximate inference in the first place. Instead, we maximize an alternative objective function, the evidence lower bound (ELBO), which is expressed as
$$ \begin{align*} \mathrm{ELBO}(q) & = \mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})} [ \log p_{\theta}(\mathbf{x} | \mathbf{z}) + \log p(\mathbf{z}) - \log q_{\phi}(\mathbf{z} | \mathbf{x}) ] \newline & = \mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})} [ \log p_{\theta}(\mathbf{x} | \mathbf{z}) ] - \mathrm{KL} [ q_{\phi}(\mathbf{z} | \mathbf{x}) || p(\mathbf{z}) ]. \end{align*} $$
Importantly, the ELBO is a lower bound to the log marginal likelihood. Therefore, maximizing it with respect to the model parameters $\theta$ approximately maximizes the log marginal likelihood. Additionally, maximizing it with respect to variational parameters $\phi$ can be shown to minimize $\mathrm{KL} [q_{\phi}(\mathbf{z} | \mathbf{x}) || p_{\theta}(\mathbf{z} | \mathbf{x}) ]$. Also, it turns out that the KL divergence determines the tightness of the lower bound, where we have equality iff the KL divergence is zero, which happens iff $q_{\phi}(\mathbf{z} | \mathbf{x}) = p_{\theta}(\mathbf{z} | \mathbf{x})$. Hence, simultaneously maximizing it with respect to $\theta$ and $\phi$ gets us two birds with one stone.
Next we discuss the form of the approximate posterior $q_{\phi}(\mathbf{z} | \mathbf{x})$, which can be viewed as a probabilistic encoder. Its role is opposite to that of the decoder. Given an observation $\mathbf{x}$, it “encodes” it into a distribution over its hidden lower-dimensional representations.
Encoder
For each local observed variable $\mathbf{x}_n$, we wish to approximate the true posterior distribution $p(\mathbf{z}_n|\mathbf{x}_n)$ over its corresponding local latent variables $\mathbf{z}_n$. A common approach is to approximate it using a variational distribution $q_{\lambda_n}(\mathbf{z}_n)$, specified as a diagonal Gaussian, where the local variational parameters $\lambda_n = \{ \boldsymbol{\mu}_n, \boldsymbol{\sigma}_n \}$ are the mean and standard deviation of this approximating distribution, $$ q_{\lambda_n}(\mathbf{z}_n) = \mathcal{N}( \mathbf{z}_n | \boldsymbol{\mu}_n, \mathrm{diag}(\boldsymbol{\sigma}_n^2) ). $$ This approach has a number of shortcomings. First, the number of local variational parameters we need to optimize grows with the size of the dataset. Second, a new set of local variational parameters need to be optimized for new unseen test points. This is not to mention the strong factorization assumption we make by specifying diagonal Gaussian distributions as the family of approximations. The last is still an active area of research, and the first two can be addressed by introducing a further approximation using an inference network.
Inference network
We amortize the cost of inference by introducing an inference network which approximates the local variational parameters $\lambda_n$ for a given local observed variable $\textbf{x}_n$. For our approximating distribution in particular, given $\textbf{x}_n$ the inference network yields two vector-valued outputs $\boldsymbol{\mu}_{\phi}(\textbf{x}_n)$ and $\boldsymbol{\sigma}_{\phi}(\textbf{x}_n)$, which we use to approximate its local variational parameters $\boldsymbol{\mu}_n$ and $\boldsymbol{\sigma}_n$, respectively. Our approximate posterior distribution now becomes $$ q_{\phi}(\mathbf{z}_n | \mathbf{x}_n) = \mathcal{N}(\mathbf{z}_n | \boldsymbol{\mu}_{\phi}(\mathbf{x}_n), \mathrm{diag}(\boldsymbol{\sigma}_{\phi}^2(\mathbf{x}_n)) ). $$ Instead of learning local variational parameters $\lambda_n$ for each data-point, we now learn a fixed number of global variational parameters $\phi$ which constitute the parameters (i.e. weights) of the inference network. Moreover, this approximation allows statistical strength to be shared across observed data-points and also generalize to unseen test points.
We specify the mean $\boldsymbol{\mu}_{\phi}(\mathbf{x})$ and log variance $\log \boldsymbol{\sigma}_{\phi}^2(\mathbf{x})$ of this distribution as the output of an inference network. For this post, we keep the architecture of the network simple, with only a single hidden layer and two fully-connected output layers. Again, this is simple to define in Keras:
# input layer
x = Input(shape=(original_dim,))
# hidden layer
h = Dense(intermediate_dim, activation='relu')(x)
# output layer for mean and log variance
z_mu = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
Since this network has multiple outputs, we couldn’t use the Sequential model API as we did for the decoder. Instead, we will resort to the more powerful Functional API, which allows us to implement complex models with shared layers, multiple inputs, multiple outputs, and so on.
Note that we output the log variance instead of the standard deviation because this is not only more convenient to work with, but also helps with numerical stability. However, we still require the standard deviation later. To recover it, we simply implement the appropriate transformation and encapsulate it in a Lambda layer.
# normalize log variance to std dev
z_sigma = Lambda(lambda t: K.exp(.5*t))(z_log_var)
Before moving on, we give a few words on nomenclature and context. In the prelude and title of this section, we characterized the approximate posterior distribution with an inference network as a probabilistic encoder (analogously to its counterpart, the probabilistic decoder). Although this is an accurate interpretation, it is a limited one. Classically, inference networks are known as recognition models, and have now been used for decades in a wide variety of probabilistic methods. When composed end-to-end, the recognition-generative model combination can be seen as having an autoencoder structure. Indeed, this structure contains the variational autoencoder as a special case, and also the now less fashionable Helmholtz machine 4. Even more generally, this recognition-generative model combination constitutes a widely-applicable approach currently known as amortized variational inference, which can be used to perform approximate inference in models that lie beyond even the large class of deep latent Gaussian models.
Having specified all the ingredients necessary to carry out variational inference (namely, the prior, likelihood and approximate posterior), we next focus on finalizing the definition of the (negative) ELBO as our loss function in Keras. As written earlier, the ELBO can be decomposed into two terms, $\mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})} [ \log p_{\theta}(\mathbf{x} | \mathbf{z}) ]$ the expected log likelihood (ELL) over $q_{\phi}(\mathbf{z} | \mathbf{x})$, and $- \mathrm{KL} [q_{\phi}(\mathbf{z} | \mathbf{x}) || p(\mathbf{z}) ]$ the negative KL divergence between prior $p(\mathbf{z})$ and approximate posterior $q_{\phi}(\mathbf{z} | \mathbf{x})$. We first turn our attention to the KL divergence term.
KL Divergence
Intuitively, maximizing the negative KL divergence term encourages approximate posterior densities that place its mass on configurations of the latent variables which are closest to the prior. Effectively, this regularizes the complexity of latent space. Now, since both the prior $p(\mathbf{z})$ and approximate posterior $q_{\phi}(\mathbf{z} | \mathbf{x})$ are Gaussian, the KL divergence can actually be calculated with the closed-form expression,
$$ \mathrm{KL} [ q_{\phi}(\mathbf{z} | \mathbf{x}) || p(\mathbf{z}) ] = - \frac{1}{2} \sum_{k=1}^K { 1 + \log \sigma_k^2 - \mu_k^2 - \sigma_k^2 } $$
where $\mu_k$ and $\sigma_k$ are the $k$-th components of output vectors $\mu_{\phi}(\mathbf{x})$ and $\sigma_{\phi}(\mathbf{x})$, respectively. This is not too difficult to derive, and I would recommend verifying this as an exercise. You can also find a derivation in the appendix of Kingma and Welling’s (2014) paper 1.
Recall that earlier, we defined the expected log likelihood term of the ELBO as
a Keras loss. We were able to do this since the log likelihood is a function of
the network’s final output (the predicted probabilities), so it maps nicely to a
Keras loss. Unfortunately, the same does not apply for the KL divergence term,
which is a function of the network’s intermediate layer outputs, the mean mu
and log variance log_var.
We define an auxiliary custom Keras layer
which takes mu and log_var as input and simply returns them as output
without modification. We do however explicitly introduce the
side-effect of
calculating the KL divergence and adding it to a collection of losses, by
calling the method add_loss 12.
class KLDivergenceLayer(Layer):
""" Identity transform layer that adds KL divergence
to the final model loss.
"""
def __init__(self, *args, **kwargs):
self.is_placeholder = True
super(KLDivergenceLayer, self).__init__(*args, **kwargs)
def call(self, inputs):
mu, log_var = inputs
kl_batch = - .5 * K.sum(1 + log_var -
K.square(mu) -
K.exp(log_var), axis=-1)
self.add_loss(K.mean(kl_batch), inputs=inputs)
return inputs
Next we feed z_mu and z_log_var through this layer (this needs to take
place before feeding z_log_var through the Lambda layer to recover z_sigma).
z_mu, z_log_var = KLDivergenceLayer()([z_mu, z_log_var])
Now when the Keras model is finally compiled, the collection of losses will be
aggregated and added to the specified Keras loss function to form the loss we
ultimately minimize. If we specify the loss as the negative log-likelihood we
defined earlier (nll), we recover the negative ELBO as the final loss we
minimize, as intended.
Side note: Alternative divergences
A key benefit of encapsulating the divergence in an auxiliary layer is that we can easily implement and swap in other divergences, such as the $\chi$-divergence or the $\alpha$-divergence. Using alternative divergences for variational inference is an active research topic 13 14.
Side note: Implicit models and adversarial learning
Additionally, we could also extend the divergence layer to use an auxiliary density ratio estimator function, instead of evaluating the KL divergence in the analytical form above. This relaxes the requirement on approximate posterior $q_{\phi}(\mathbf{z}|\mathbf{x})$ (and incidentally also prior $p(\mathbf{z})$) to yield tractable densities, at the cost of maximizing a cruder estimate of the ELBO. This is known as Adversarial Variational Bayes10, and is an important line of recent research that, when taken to its logcal conclusion, can extend the applicability of variational inference to arbitrarily expressive implicit probabilistic models with intractable likelihoods11.
Reparameterization using Merge Layers
To perform gradient-based optimization of ELBO with respect to model parameters $\theta$ and variational parameters $\phi$, we require its gradients with respect to these parameters, which is generally intractable. Currently, the dominant approach for circumventing this is by Monte Carlo (MC) estimation of the gradients. The basic idea is to write the gradient of the ELBO as an expectation of the gradient, approximate it with MC estimates, then perform stochastic gradient descent with the repeated MC gradient estimates.
There exist a number of estimators based on different variance reduction techniques. However, MC gradient estimates based on the reparameterization trick, known as the reparameterization gradients, have be shown to have the lowest variance among competing estimators for continuous latent variables5. The reparameterization trick is a straightforward change of variables that expresses the random variable $\mathbf{z} \sim q_{\phi}(\mathbf{z} | \mathbf{x})$ as a deterministic transformation $g_{\phi}$ of another random variable $\boldsymbol{\epsilon}$ and input $\mathbf{x}$, with parameters $\phi$,
$$ z = g_{\phi}(\mathbf{x}, \boldsymbol{\epsilon}), \quad \boldsymbol{\epsilon} \sim p(\boldsymbol{\epsilon}). $$
Note that $p(\boldsymbol{\epsilon})$ is simpler base distribution which is parameter-free and independent of $\mathbf{x}$ or $\phi$. To prevent clutter, we write the ELBO as an expectation of the function $f(\mathbf{x}, \mathbf{z}) = \log p_{\theta}(\mathbf{x} , \mathbf{z}) - \log q_{\phi}(\mathbf{z} | \mathbf{x})$ over distribution $q_{\phi}(\mathbf{z} | \mathbf{x})$. Now, for any function $f(\mathbf{x}, \mathbf{z})$, taking the gradient of the expectation with respect to $\phi$, and substituting all occurrences of $\mathbf{z}$ with $g_{\phi}(\mathbf{x}, \boldsymbol{\epsilon})$, we have
$$ \begin{align*} \nabla_{\phi} \mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})} [ f(\mathbf{x}, \mathbf{z}) ] & = \nabla_{\phi} \mathbb{E}_{p(\boldsymbol{\epsilon})} [ f(\mathbf{x}, g_{\phi}(\mathbf{x}, \boldsymbol{\epsilon})) ] \newline & = \mathbb{E}_{p(\mathbf{\epsilon})} [ \nabla_{\phi} f(\mathbf{x}, g_{\phi}(\mathbf{x}, \boldsymbol{\epsilon})) ]. \end{align*} $$
In other words, this simple reparameterization allows the gradient and the expectation to commute, thereby allowing us to compute unbiased stochastic estimates of the ELBO gradients by drawing noise samples $\boldsymbol{\epsilon}$ from $p(\boldsymbol{\epsilon})$.
To recover the diagonal Gaussian approximation we specified earlier $q_{\phi}(\mathbf{z}_n | \mathbf{x}_n) = \mathcal{N}(\mathbf{z}_n | \boldsymbol{\mu}_{\phi}(\mathbf{x}_n), \mathrm{diag}(\boldsymbol{\sigma}_{\phi}^2(\mathbf{x}_n)))$, we draw noise from the Normal base distribution, and specify a simple location-scale transformation
$$ \mathbf{z} = g_{\phi}(\mathbf{x}, \boldsymbol{\epsilon}) = \mu_{\phi}(\mathbf{x}) + \sigma_{\phi}(\mathbf{x}) \odot \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), $$
where $\mu_{\phi}(\mathbf{x})$ and $\sigma_{\phi}(\mathbf{x})$ are the outputs
of the inference network defined earlier with parameters $\phi$, and $\odot$
denotes the elementwise product. In Keras, we explicitly make the noise vector
an input to the model by defining an Input layer for it. We then implement the
above location-scale transformation using Merge layers, namely Add and Multiply.
eps = Input(shape=(latent_dim,))
z_eps = Multiply()([z_sigma, eps])
z = Add()([z_mu, z_eps])
Side note: Monte Carlo sample size
Note both the inputs for observed variables and noise (x and eps) need to be
specified explicitly as inputs to our final model.
Furthermore, the size of their first dimension (i.e. batch size) are required
to be the same.
This corresponds to using a exactly one Monte Carlo sample to approximate the
expected log likelihood, drawing a single sample $\mathbf{z}_n$ from
$q_{\phi}(\mathbf{z}_n | \mathbf{x}_n)$ for each data-point $\mathbf{x}_n$ in
the batch. Although you might find an MC sample size of 1 surprisingly small,
it is actually adequate for a sufficiently large batch size (~100) 1.
In a follow-up post,
I demonstrate how to extend our approach to support larger MC sample sizes using
just a few minor tweaks. This extension is crucial for implementing the
importance weighted autoencoder 8.
Now, since the noise input is drawn from the Normal distribution, we can save
from having to feed in values for this input from outside the computation graph
by binding a tensor to this Input layer. Specifically, we bind a tensor created
using K.random_normal with the required shape,
eps = Input(tensor=K.random_normal(shape=(K.shape(x)[0], latent_dim)))
While eps still needs to be explicitly specified as an input to compile the
model, values for this input will no longer be expected by methods such as
fit, predict. Instead, samples from this distribution will be lazily
generated inside the computation graph when required. See my notes on
Keras Constant Input Layers with Fixed Source of Stochasticity for more
details.
In the example implementation, all of this logic is encapsulated in a single
Lambda layer, which simultaneously draws samples from a hard-coded base
distribution and also performs the location-scale transformation.
In contrast, this approach achieves a good level of
loose coupling
and separation of concerns.
By decoupling the random noise vector from the layer’s internal logic and
explicitly making it a model input, we emphasize the fact that all sources of
stochasticity emanate from this input. It thereby becomes clear that a random
sample drawn from a particular approximating distribution is obtained by feeding
this source of stochasticity through a number of successive deterministic
transformations.
Side notes: Gumbel-softmax trick for discrete latent variables
As an example, we could provide samples drawn from the Uniform distribution as noise input. By applying a number of deterministic transformations that constitute the Gumbel-softmax reparameterization trick 9, we are able to obtain samples from the Categorical distribution. This allows us to perform approximate inference on discrete latent variables, and can be implemented in this framework by adding a dozen or so lines of code!
Putting it all together
So far, we’ve dissected the variational autoencoder into modular components and discussed the role and implementation of each one at some length. Now let’s compose these components together end-to-end to form the final autoencoder architecture.
x = Input(shape=(original_dim,))
h = Dense(intermediate_dim, activation='relu')(x)
z_mu = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
z_mu, z_log_var = KLDivergenceLayer()([z_mu, z_log_var])
z_sigma = Lambda(lambda t: K.exp(.5*t))(z_log_var)
eps = Input(tensor=K.random_normal(shape=(K.shape(x)[0], latent_dim)))
z_eps = Multiply()([z_sigma, eps])
z = Add()([z_mu, z_eps])
decoder = Sequential([
Dense(intermediate_dim, input_dim=latent_dim, activation='relu'),
Dense(original_dim, activation='sigmoid')
])
x_pred = decoder(z)
It’s surprisingly concise, taking up around 20 lines of code. The diagram of the full model architecture is visualized below.
Finally, we specify and compile the model, using the negative log likelihood
nll defined earlier as the loss.
vae = Model(inputs=[x, eps], outputs=x_pred)
vae.compile(optimizer='rmsprop', loss=nll)
Model fitting
Dataset: MNIST digits
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(-1, original_dim) / 255.
x_test = x_test.reshape(-1, original_dim) / 255.
vae.fit(x_train,
x_train,
shuffle=True,
epochs=epochs,
batch_size=batch_size,
validation_data=(x_test, x_test))
Loss (NELBO) convergence
pd.DataFrame(hist.history).plot(ax=ax)
Model evaluation
encoder = Model(x, z_mu)
# display a 2D plot of the digit classes in the latent space
z_test = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(z_test[:, 0], z_test[:, 1], c=y_test,
alpha=.4, s=3**2, cmap='viridis')
plt.colorbar()
plt.show()

# display a 2D manifold of the digits
n = 15 # figure with 15x15 digits
digit_size = 28
# linearly spaced coordinates on the unit square were transformed
# through the inverse CDF (ppf) of the Gaussian to produce values
# of the latent variables z, since the prior of the latent space
# is Gaussian
z1 = norm.ppf(np.linspace(0.01, 0.99, n))
z2 = norm.ppf(np.linspace(0.01, 0.99, n))
z_grid = np.dstack(np.meshgrid(z1, z2))
x_pred_grid = decoder.predict(z_grid.reshape(n*n, latent_dim)) \
.reshape(n, n, digit_size, digit_size)
plt.figure(figsize=(10, 10))
plt.imshow(np.block(list(map(list, x_pred_grid))), cmap='gray')
plt.show()

Recap
In this post, we covered the basics of amortized variational inference, looking at variational autoencoders as a specific example. In particular, we
- Implemented the decoder and encoder using the Sequential and functional Model API respectively.
- Augmented the final loss with the KL divergence term by writing an auxiliary custom layer.
- Worked with the log variance for numerical stability, and used a Lambda layer to transform it to the standard deviation when necessary.
- Explicitly made the noise an Input layer, and implemented the reparameterization trick using Merge layers.
- Fixed the noise input to a stochastic tensor, so random samples are generated within the computation graph.
What’s next
Next, we will extend the divergence layer to use an auxiliary density ratio estimator function, instead of evaluating the KL divergence in the analytical form above. This relaxes the requirement on approximate posterior $q_{\phi}(\mathbf{z}|\mathbf{x})$ (and incidentally also prior $p(\mathbf{z})$) to yield tractable densities, at the cost of maximizing a cruder estimate of the ELBO. This is known as Adversarial Variational Bayes10, and is an important line of recent research that, when taken to its logcal conclusion, can extend the applicability of variational inference to arbitrarily expressive implicit probabilistic models with intractable likelihoods11.
Cite as:
@article{tiao2017vae,
title = "{A} {T}utorial on {V}ariational {A}utoencoders with a {C}oncise {K}eras {I}mplementation",
author = "Tiao, Louis C",
journal = "tiao.io",
year = "2017",
url = "https://tiao.io/post/tutorial-on-variational-autoencoders-with-a-concise-keras-implementation/"
}
To receive updates on more posts like this, follow me on Twitter and GitHub!
Links & Resources
Below, you can find:
- The accompanying Jupyter Notebook used to generate the diagrams and plots in this post.
- The above snippets combined in a single executable Python file:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from keras import backend as K
from keras.layers import Input, Dense, Lambda, Layer, Add, Multiply
from keras.models import Model, Sequential
from keras.datasets import mnist
original_dim = 784
intermediate_dim = 256
latent_dim = 2
batch_size = 100
epochs = 50
epsilon_std = 1.0
def nll(y_true, y_pred):
""" Negative log likelihood (Bernoulli). """
# keras.losses.binary_crossentropy gives the mean
# over the last axis. we require the sum
return K.sum(K.binary_crossentropy(y_true, y_pred), axis=-1)
class KLDivergenceLayer(Layer):
""" Identity transform layer that adds KL divergence
to the final model loss.
"""
def __init__(self, *args, **kwargs):
self.is_placeholder = True
super(KLDivergenceLayer, self).__init__(*args, **kwargs)
def call(self, inputs):
mu, log_var = inputs
kl_batch = - .5 * K.sum(1 + log_var -
K.square(mu) -
K.exp(log_var), axis=-1)
self.add_loss(K.mean(kl_batch), inputs=inputs)
return inputs
decoder = Sequential([
Dense(intermediate_dim, input_dim=latent_dim, activation='relu'),
Dense(original_dim, activation='sigmoid')
])
x = Input(shape=(original_dim,))
h = Dense(intermediate_dim, activation='relu')(x)
z_mu = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
z_mu, z_log_var = KLDivergenceLayer()([z_mu, z_log_var])
z_sigma = Lambda(lambda t: K.exp(.5*t))(z_log_var)
eps = Input(tensor=K.random_normal(stddev=epsilon_std,
shape=(K.shape(x)[0], latent_dim)))
z_eps = Multiply()([z_sigma, eps])
z = Add()([z_mu, z_eps])
x_pred = decoder(z)
vae = Model(inputs=[x, eps], outputs=x_pred)
vae.compile(optimizer='rmsprop', loss=nll)
# train the VAE on MNIST digits
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(-1, original_dim) / 255.
x_test = x_test.reshape(-1, original_dim) / 255.
vae.fit(x_train,
x_train,
shuffle=True,
epochs=epochs,
batch_size=batch_size,
validation_data=(x_test, x_test))
encoder = Model(x, z_mu)
# display a 2D plot of the digit classes in the latent space
z_test = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(z_test[:, 0], z_test[:, 1], c=y_test,
alpha=.4, s=3**2, cmap='viridis')
plt.colorbar()
plt.show()
# display a 2D manifold of the digits
n = 15 # figure with 15x15 digits
digit_size = 28
# linearly spaced coordinates on the unit square were transformed
# through the inverse CDF (ppf) of the Gaussian to produce values
# of the latent variables z, since the prior of the latent space
# is Gaussian
u_grid = np.dstack(np.meshgrid(np.linspace(0.05, 0.95, n),
np.linspace(0.05, 0.95, n)))
z_grid = norm.ppf(u_grid)
x_decoded = decoder.predict(z_grid.reshape(n*n, 2))
x_decoded = x_decoded.reshape(n, n, digit_size, digit_size)
plt.figure(figsize=(10, 10))
plt.imshow(np.block(list(map(list, x_decoded))), cmap='gray')
plt.show()
D. P. Kingma and M. Welling, “Auto-Encoding Variational Bayes,” in Proceedings of the 2nd International Conference on Learning Representations (ICLR), 2014. ↩︎ ↩︎ ↩︎
Section “Recognition models and amortised inference” in Shakir’s blog post ↩︎
Dayan, P., Hinton, G. E., Neal, R. M., & Zemel, R. S. (1995). The Helmholtz machine. Neural Computation, 7(5), 889–904. http://doi.org/10.1162/neco.1995.7.5.889 ↩︎ ↩︎
Rezende, D. J., Mohamed, S., & Wierstra, D. (2014). “Stochastic backpropagation and approximate inference in deep generative models,” in Proceedings of The 31st International Conference on Machine Learning, 2014, (Vol. 32, pp. 1278–1286). Bejing, China: PMLR. http://doi.org/10.1051/0004-6361/201527329 ↩︎ ↩︎ ↩︎ ↩︎
For a complete treatment of variational autoencoders, and variational inference in general, I highly recommend:
- Jaan Altosaar’s blog post, What is a variational autoencoder?
- Diederik P. Kingma’s PhD Thesis, Variational Inference and Deep Learning: A New Synthesis.
D. Rezende and S. Mohamed, “Variational Inference with Normalizing Flows,” in Proceedings of the 32nd International Conference on Machine Learning, 2015, vol. 37, pp. 1530–1538. ↩︎
Y. Burda, R. Grosse, and R. Salakhutdinov, “Importance Weighted Autoencoders,” in Proceedings of the 3rd International Conference on Learning Representations (ICLR), 2015. ↩︎ ↩︎
E. Jang, S. Gu, and B. Poole, “Categorical Reparameterization with Gumbel-Softmax,” Nov. 2016. in Proceedings of the 5th International Conference on Learning Representations (ICLR), 2017. ↩︎ ↩︎
L. Mescheder, S. Nowozin, and A. Geiger, “Adversarial Variational Bayes: Unifying Variational Autoencoders and Generative Adversarial Networks,” in Proceedings of the 34th International Conference on Machine Learning, 2017, vol. 70, pp. 2391–2400. ↩︎ ↩︎ ↩︎
D. Tran, R. Ranganath, and D. Blei, “Hierarchical Implicit Models and Likelihood-Free Variational Inference,” in Advances in Neural Information Processing Systems 30, 2017. ↩︎ ↩︎ ↩︎
To support sample weighting (fined-tuning how much each data-point contributes to the loss), Keras losses are expected returns a scalar for each data-point in the batch. In contrast, losses appended with the
add_lossmethod don’t support this, and are expected to be a single scalar. Hence, we calculate the KL divergence for all data-points in the batch and take the mean before passing it toadd_loss. ↩︎Y. Li and R. E. Turner, “Rényi Divergence Variational Inference,” in Advances in Neural Information Processing Systems 29, 2016. ↩︎
A. B. Dieng, D. Tran, R. Ranganath, J. Paisley, and D. Blei, “Variational Inference via chi Upper Bound Minimization,” in Advances in Neural Information Processing Systems 30, 2017. ↩︎