NumPy mgrid vs. meshgrid

The meshgrid function is useful for creating coordinate arrays to vectorize function evaluations over a grid. Experienced NumPy users will have noticed some discrepancy between meshgrid and the mgrid, a function that is used just as often, for exactly the same purpose. What is the discrepancy, and why does a discrepancy even exist when¹ “there should be one – and preferably only one – obvious way to do it.”

First, recall that meshgrid behaves as follows:

>>> import numpy as np
>>> x1, y1 = np.meshgrid(np.arange(1, 11, 2), np.arange(-12, -3, 3))
>>> x1 # 3x5 array
array([[1, 3, 5, 7, 9],
       [1, 3, 5, 7, 9],
       [1, 3, 5, 7, 9]])
>>> y1 # 3x5 array
array([[-12, -12, -12, -12, -12],
       [ -9,  -9,  -9,  -9,  -9],
       [ -6,  -6,  -6,  -6,  -6]])

If you have used NumPy for a while or are familiar enough with how Broadcasting works, you will have realized that meshgrid is actually superfluous for NumPy arrays, and that it is actually just an implementation of MATLAB’s meshgrid, probably to cater to users coming from a MATLAB background.

Observe the behavior of mgrid, which essentially returns the transpose of meshgrid:

>>> x2, y2 = np.mgrid[1:11:2, -12:-3:3]
>>> x2 # 5x3 array
array([[1, 1, 1],
       [3, 3, 3],
       [5, 5, 5],
       [7, 7, 7],
       [9, 9, 9]])
>>> y2 # 5x3 array
array([[-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6]])
>>> np.all(x1 == x2.T)
True
>>> np.all(y2 == y2.T)
True

Note this this order is actually more natural, since mgrid just fleshes out the open (not fleshed out) grids given by ogrid by broadcasting them to form dense grids, i.e.

>>> a, b = np.ogrid[1:11:2, -12:-3:3]
>>> a # 5x1 array
array([[1],
       [3],
       [5],
       [7],
       [9]])
>>> b # 1x3 array
array([[-12,  -9,  -6]])

and the 5x1 array a is broadcasted with the 1x3 array b to form two 5x3 arrays

>>> x2, y2 = np.broadcast_arrays(a, b)
>>> x2 # 5x3 array
array([[1, 1, 1],
       [3, 3, 3],
       [5, 5, 5],
       [7, 7, 7],
       [9, 9, 9]])
>>> y2 # 5x3 array
array([[-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6],
       [-12,  -9,  -6]])

which behaves exactly the same way as mgrid. Note that you seldom have to broadcast arrays explicitly, let alone use functions like mgrid or meshgrid, since all arithmetic operations on NumPy arrays already perform broadcasting implicitly. E.g.

>>> x2 + y2 # adding two 5x3 arrays
array([[-11,  -8,  -5],
       [ -9,  -6,  -3],
       [ -7,  -4,  -1],
       [ -5,  -2,   1],
       [ -3,   0,   3]])
>>> a + b # adding a 5x1 array to a 1x3 array
array([[-11,  -8,  -5],
       [ -9,  -6,  -3],
       [ -7,  -4,  -1],
       [ -5,  -2,   1],
       [ -3,   0,   3]])

Finally, if for some reason you must have output like that of meshgrid, just use mgrid with the arguments and unpacking targets reversed.

>>> y3, x3 = np.mgrid[-12:-3:3, 1:11:2]
>>> x3 # 3x5 array
array([[1, 3, 5, 7, 9],
       [1, 3, 5, 7, 9],
       [1, 3, 5, 7, 9]])
>>> y3 # 3x5 array
array([[-12, -12, -12, -12, -12],
       [ -9,  -9,  -9,  -9,  -9],
       [ -6,  -6,  -6,  -6,  -6]])
>>> np.all(x1 == x3)
True
>>> np.all(y1 == y3)
True

Uniformly-spaced meshgrids

At the very beginning, we created a meshgrid by specifying ranges and step lengths using np.arange. Suppose instead we just want to specify the number of evenly-spaced points we’d like the meshgrid to include between some ranges. In other words, we’re instead interested in using np.linspace instead of np.arange:

>>> x1, y1 = np.meshgrid(np.linspace(-5, 5, 5), 
...                      np.linspace(-12, -3, 3))
>>> x1 # 3x5 array
array([[-5. , -2.5,  0. ,  2.5,  5. ],
       [-5. , -2.5,  0. ,  2.5,  5. ],
       [-5. , -2.5,  0. ,  2.5,  5. ]])
>>> y1 # 3x5 array
array([[-12. , -12. , -12. , -12. , -12. ],
       [ -7.5,  -7.5,  -7.5,  -7.5,  -7.5],
       [ -3. ,  -3. ,  -3. ,  -3. ,  -3. ]])

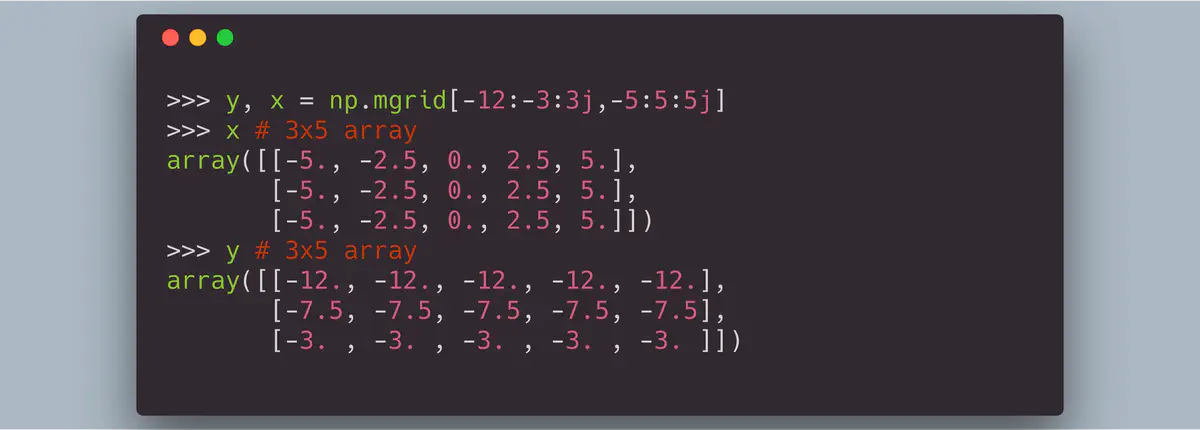
The mgrid allows you to specify this by using a complex number (e.g. 5j) as a step length. When the step length is a complex number, the integer part of its magnitude is interpreted as specifying the number of points to create between the start and stop values, where the stop value is inclusive. Hence, to achieve the above using mgrid:

>>> y3, x3 = np.mgrid[-12:-3:3j,-5:5:5j]
>>> np.all(x1 == x3)
True
>>> np.all(y1 == y3)
True

In summary, while the mgrid function is often overlooked, it is very general and powerful, and subsumes many other functions in NumPy as special cases. It is related to the ogrid, and demonstrates the flexibility of NumPy Broadcasting.

Further Reading

• http://stackoverflow.com/questions/12402045/mesh-grid-functions-in-python-meshgrid-mgrid-ogrid-ndgrid